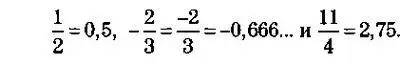Gustavo Pineiro - Бесчисленное поддается подсчету. Кантор. Бесконечность в математике.

Продолжим рассмотрение статьи Кантора 1874 года. Мы уже знаем, что множество всех натуральных чисел эквивалентно множеству квадратных чисел. Обратимся теперь к целым числам.

В их множество входят натуральные и отрицательные числа: -1, —2, —3, —4, ... Такое множество, как и квадратные числа, эквивалентно натуральным. Чтобы доказать это, достаточно продемонстрировать взаимно однозначное соответствие этих групп.

Предположим, что мы сопоставляем Ос 0, 1 с -1, 2 с -2, 3 с -3 и так далее.

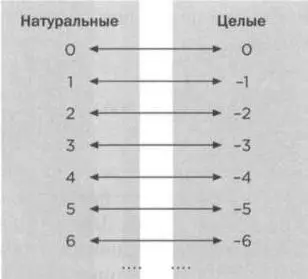
Эта попытка провалится, так как в правой колонке не все числа будут целые, то есть некоторые целые числа останутся без пары. Но тот факт, что это решение неверное, не означает, что не существует правильного разбиения на пары. Действительно, если мы соотнесем натуральные числа 0,1,2,3,4,5,6,... с целыми 0,1, -1, 2, -2,3, -3,..., то получим взаимно однозначное соответствие между ними.

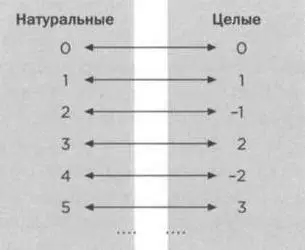
Кардинальное число целых чисел всегда будет *********... Следующая группа, которую мы должны рассмотреть, состоит из рациональных чисел. Слово «рациональный» происходит от латинского ratio, что означает и «разум», и «отношение», «деление». Таким образом, рациональные числа — это такие числа, которые можно записать в виде соотношения двух целых чисел (в математике их еще называют дробями). Рациональными являются числа

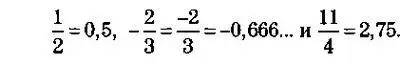
Целые числа также являются рациональными, например 3/1 = 3 и 0/1 = 0 (выражение 0/0 не представляет никакого рационального числа, как и 1/0, 2/0, 3/0...). Следовательно, мы можем доказать, что множество рациональных чисел включает в себя и множество целых чисел, которое, в свою очередь, включает множество натуральных чисел. И тем не менее между множеством рациональных чисел, с одной стороны, и множеством натуральных и целых чисел, с другой, есть фундаментальное различие. Чтобы объяснить его суть, нам понадобится числовая ось. Это прямая (ее можно представить себе как потенциально, так и как актуально бесконечную), на которой отмечены числа. Сначала выберем произвольную точку и отметим на ней число 0, а потом еще одну, на которой отметим 1.

Каждая из этих точек на самом деле является математической, то есть не обладает длиной, но в данном случае, чтобы сделать их видимыми, мы обозначим их маленькими окружностями.

Выбор места для точек 0 и 1 совершенно произволен, но, сделав его, мы обусловим расположение остальных чисел. Расстояние между 0 и 1 должно равняться расстоянию между 1 и 2, а также расстоянию между 2 и 3 и так далее. То же справедливо и для отрицательных чисел.

Георг Кантор в 1870 году по прибытии в Галльский университет.

Университет в Галле, приблизительно 1936 год.

Портрет Рихарда Дедекинда. Генрих Кенигсдорф, 1927 год.

Портрет Карла Теодора Вильгельма Вейерштрасса. Конрад Фер.

Немецкий математик Давид Гильберт (1862-1943) придумал задачу, в которой упрощенно излагается одно из следствий теории Кантора. Представим себе отель, в котором есть бесконечное количество комнат, обозначенных номерами 1, 2, 3, 4, 5 и так далее. В каждом номере есть постояльцы, которых мы для удобства так же обозначим числами 1, 2, 3, 4, 5 и так далее. Однажды в отель приезжает новый гость, назовем его Господином 0, но все номера заняты, а по правилам отеля двое людей не могут занимать один номер. Господин 0 уже собирается уходить, когда ему предлагают такой вариант: он поселится в номере 1, гость 1 — в номере 2, гость 2 — в номере 3 и так далее. Таким образом, Господин 0 сможет остановиться в отеле, и никто не останется без комнаты.