Terence Hines - Pseudoscience and the Paranormal

Using the appropriate statistical test (called chi square ), the details of which can be found in any statistics textbook, we can figure out the likelihood that the several hypothetical results of the extrovert-introvert experiment described above would occur by chance. This is shown in the table below.

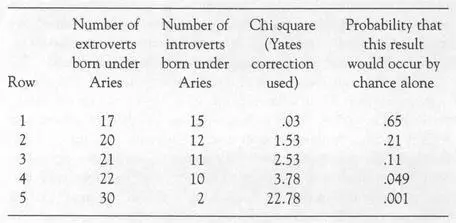
The table can be interpreted as follows. If we conducted the experiment described above and obtained the results shown in row 1, there would be no basis for saying that astrological influence was at work. The difference here between the number of extroverts and introverts born under Aries is 2, and the statistics tell us that a difference of that size or less would occur purely by chance 65 percent of the time. Here, the statistics merely confirm our intuition that the result is unimpressive as evidence for astrology. Consider the results in row 5. Here again, the statistics confirm the obvious—these results are very unlikely to be due to chance alone. Such results would occur by chance alone only 1 time in 1,000. If our experiment actually yielded such results, we could be pretty confident that something was going on.

Statistical analyses are most valuable where it is not immediately obvious on inspection of the data whether the results are due to chance factors or not. Rows 2, 3, and 4 are examples. In all three rows, there are more extroverts than introverts born under Aries, but only the results in row 4 could convince the investigator that some nonchance factor, perhaps astrological influence, was involved. The difference in Row 2 is 8, but a difference of 8 or less would be obtained purely by chance fully 21 percent of the time in such an experiment. This is probably a somewhat higher figure that you might have guessed. In Row 3 the difference is 10, but this difference would be obtained 11 times out of 100 by chance and does not reach the standard criterion that a result must occur by chance 5 times or fewer in 100 to be considered as due—to nonchance factors. In row 4, this criterion is met. The difference is 12, and such a difference would occur fewer than 5 times in 100 by chance. Here, as in row 5, we would be justified in attributing to some nonchance factor the differences in the number of introverts and extroverts born under Aries.

Statistical analyses can tell an investigator the likelihood that a set of given results is due to chance. However, while the statistics can indicate that a result is unlikely to be due to chance, they do not indicate what nonchance factors are responsible for the result. A nonparanormal example will illustrate this point. One semester I taught two sections of introductory psychology. One section met at 8 A.M., the other at 11 A.M. The textbook used in each section was the same; so, of course, was the instructor. I used the same sets of lecture notes for both classes and covered the same material in the same order. I gave equivalent tests to each section. These tests covered the same material to the same degree of difficulty, but used different questions. On the first test, the average score of the 8 A.M. section was 68 percent. The average score of the 11 A.M. section was 79 percent. This difference is highly significant statistically and would have occurred by chance only about 2 times in 100. The knowledge that this is a strong nonchance difference does not indicate the cause of the difference. A number of possibilities spring to mind. One is that students in the 8 A.M. section were dumber than those in the 11 A.M. section. Another possibility is that the 8 A.M. section was sleepier than the 11 A.M. section. Another possibility is that I am a better lecturer at 11 A.M. than at 8 A.M. Or perhaps a combination of these factors is responsible for the difference observed. Interestingly, the difference was maintained throughout the term. To determine what nonchance factor is responsible for the observed difference is an experimental question that cannot be answered just by pointing to the fact that the difference is statistically significant.

That is why, in the discussion above of the extrovert-introvert experiment, I kept referring to “nonchance factors,” rather than directly attributing the differences in numbers of the two personality types born under Aries to astrological factors—even when the differences were clearly statistically significant. It is certainly possible, for example, to imagine obtaining the results in rows 4 or 5 even with no astrological influence operating at all. How? Remember that the subjects in our hypothetical experiment were recruited through advertisements in a campus paper. Extroverts are much more likely to respond to such an ad than are introverts, so we would end up with more extroverts in the sample of thirty-two subjects. The results are still statistically significant, but are obviously not due to astrological influence. It is not enough, then, to point to statistical significance as “proof” of anything. The experiment that generated the data that was subjected to statistical test must have been designed to eliminate the sort of artifactual finding of our hypothetical study.

Another important statistical point should be made here. As mentioned earlier, a “statistically significant” result is one that, according to statistical analyses, will occur by chance 5 times or fewer in 100. It could occur purely by chance, but such an occurrence would be rare. Rare events do occur, however, especially if you give them enough opportunities. In fact, rare events are almost certain to occur given sufficient opportunity. This is called the Law of Large Numbers and is responsible for much acceptance of pseudoscientific beliefs.

What is the probability of flipping a fair coin 10 times and having it come up heads all 10 times? This obviously rare event would occur only once in 2 10, or 1,024, times. But what if you flipped the coin 100,000 times? You would expect that about 97 runs of 10 successive heads would occur in that run of 100,000 coin flips. The event, 10 heads in a row, is no less rare—you’ve just given it more opportunity to occur.

Now let us assume a universe where it is absolutely certain that there are no astrological influences whatsoever. We perform a well-designed study (as opposed to the poorly designed study described above) to test whether more extroverts than introverts are born under Aries. Since in this universe there are no astrological influences, it is unlikely that we will find more extroverts than introverts born under Aries if we conduct the experiment only once. But what if we repeat it 100 times, using a different sample of subjects each time? Out of that set of 100 different experiments, we would expect to find about 5 that yield “significant” results. Why? Because “significant” is defined as a result that occurs by chance alone 5 times or fewer in 100. Given 100 opportunities to occur, such “significant” results will be obtained about 5 times.

Think about it another way. If we tested 100 different astrological predictions in our nonastrological universe, would we expect to find that none of the 100 tests showed “significant” astrological effects? No—about 5 of the 100 tests would yield results that were “significant.” Would this finding provide support for the existence of astrological influence? Certainly not—while the results are truly “significant” (that is, they are not due to poor experimental design and the like), they are not due to astrological influence. They are simply due to chance, since we would be giving these relatively rare events a large number of chances to happen. A problem appears, however, when one does numerous experiments to test, say, astrology, and reports only those that yield “significant” results, ignoring those that do not yield such results. This basically dishonest procedure is, unfortunately, all too common in the literature supporting pseudoscientific claims. Examples of these surprisingly common statistical errors will be pointed out frequently in the rest of this chapter and in succeeding chapters. Let us now return to the experimental literature on astrological predictions.