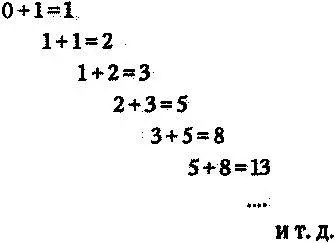Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

Левин улыбнулся и перешел к букве S. Он перенастроил свой калибр так, что зубцы касались самого верхнего и самого нижнего окончания буквы S, и, к моему полному изумлению, средний зубец попал точно на изгиб в букве S.

Точное попадание, — спокойно заметил Левин. — В почерк каждого человека заложена золотая пропорция.

Золотая пропорция — это число, которое описывает отношение, возникающее при делении отрезка на две части таким образом, что отношение всего отрезка к большему из двух равно отношению большего к меньшему. Другими словами, когда отношение А + В к А равно отношению А к В:

Деление отрезка на две части указанным образом называется золотым сечением. При этом число фи — отношение между большим и меньшим отрезками — можно вычислить, и оно равно (1 + 5√2√2√2√2)/2. Это иррациональное число, десятичное разложение которого начинается как

1,61803398874989484820…

Древних греков зачаровывало число фи. Они познакомились с ним, рассматривая пятиконечную звезду (пентаграмму), которая являлась почитаемым символом Пифагорейского братства. Евклид писал о «делении отрезка в крайнем и среднем отношении», он предложил метод построения правильного пятиугольника с помощью циркуля и линейки. Начиная с эпохи Возрождения это число интриговало как художников, так и математиков.

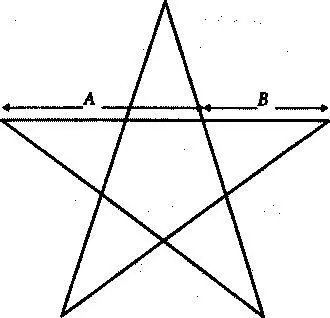
Пятиконечная звезда — мистический символ, рожденный в древности, — содержит в себе золотое сечение

Ключевой работой, посвященной золотому сечению, была написанная в 1509 году книга выдающегося итальянского математика францисканца Луки Пачоли (1445–1517) «Божественная пропорция», где описывались многие случаи появления этого числа из геометрических построений. Иллюстрировал книгу друживший с Пачоли Леонардо да Винчи. Итак, Пачоли пришел к выводу, что число фи — послание Бога, источник тайного знания о внутренней красоте вещей.

С математической точки зрения число фи интересно еще и потому, что оно связано с самой знаменитой последовательностью в математике — последовательностью Фибоначчи. Эта последовательность начинается с чисел 0 и 1, а далее каждый следующий член представляет собой сумму двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377… Вот как получаются эти числа:

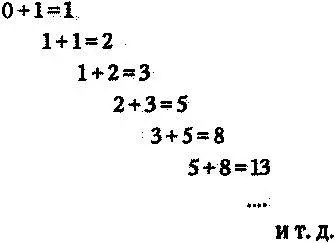
Прежде чем говорить о том, как связаны число фи и последовательность Фибоначчи, давайте изучим саму последовательность. Природа тяготеет к числам Фибоначчи. Заглянув в сад, вы обнаружите, что у большинства цветков число лепестков равно числам Фибоначчи. У лилий и ирисов — три лепестка, у гвоздик и лютиков — пять, у дельфиниума — восемь, у ноготков — 13, у астр — 21, а у маргариток — 55 или 89. Каждый цветок может и не иметь всегда в точности столько лепестков, но в среднем их число будет одним из чисел Фибоначчи. Например, на стебле клевера обычно три листочка — это тоже число Фибоначчи. Лишь очень редко у клевера бывает четыре листочка, поэтому четырехлистный клевер считается особенным. Они встречаются редко как раз потому, что 4 — не число Фибоначчи.

Числа Фибоначчи встречаются также в спиральных узорах, которые образуют чешуйки сосновых шишек и ананасов, соцветия цветной капусты и семена подсолнухов. Можно пересчитывать витки спирали по часовой стрелке или против — все, что вы насчитаете в любом направлении, будет числами Фибоначчи. На ананасах, как правило, 5 и 8 спиралей, или же 8 и 13. На еловых шишках их обычно 8 и 13. У подсолнухов спиралей может быть 21 и 34 или же 34 и 55 — хотя известны примеры с 144 и 233 спиралями. Чем больше семян в подсолнухе, тем больше оказывается число спиралей.

Последовательность Фибоначчи называется так потому, что ее члены впервые появились в написанной Фибоначчи книге «Liber Abaci», в связи с задачей о кроликах. Однако свое имя эта последовательность приобрела лишь через более чем 600 лет после выхода книги — в 1877 году, когда ее изучал теоретико-числовик Эдуар Люка. Именно он решил воздать должное Фибоначчи, назвав последовательность его именем.

В книге «Liber Abaci» эта последовательность возникла из следующей задачи. Пусть у нас имеется пара кроликов, которая через месяц дает потомство — появляется еще пара кроликов. Если у каждой взрослой пары кроликов каждый месяц появляется потомство — пара крольчат, — а крольчатам требуется один месяц, чтобы стать взрослыми, то сколько кроликов получится от первой пары через год? Ответ на этот вопрос можно получить, пересчитывая кроликов из месяца в месяц. В первый месяц имеется всего одна пара. В второй месяц — две, поскольку исходная пара произвела новую. На третий месяц имеется три пары, потому что исходная пара снова размножилась, но другая пара лишь достигла зрелости. На четвертый месяц обе пары взрослых кроликов размножились, что добавит двойку к имеющейся тройке. Последовательность Фибоначчи — это полное число пар, подсчитанное месяц за месяцем: