Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

Головоломки — это, кроме того, чудесный способ сделать математику более привлекательной. Решение их нередко требует нестандартного мышления или опирается на факты, на первый взгляд противоречащие интуиции. Ощущение достигнутого успеха, испытываемое при решении головоломок, — удовольствие, которое хочется переживать вновь и вновь; когда же задачка не решается, от тоски просто лезешь на стенку. Чувство поражения почти непереносимо.

Издатели быстро осознали, что рынок математических забав огромен. В 1612 году во Франции вышла книга Клода Гаспара Баше «Занимательные и приятные задачи (очень полезные для всех любопытных людей, использующих арифметику)». Один из ее разделов был посвящен магическим квадратам, фокусам с картами, вопросам, относящимся к системам счисления с основанием, отличным от десяти, а также задачкам из серии «задумай число». Баше был серьезным исследователем, он перевел Диофантову «Арифметику» с греческого на латынь и снабдил текст своими комментариями. Однако его популярная книга по математике оказалась, пожалуй, гораздо более заметной, чем его научные труды. Она сохраняла свою актуальность в течение столетий, а сравнительно недавно — в 1959 году — выдержала еще одно издание. Мы уже говорили, что определяющая черта математики — пусть даже развлекательной — состоит в том, что она никогда не устаревает.

В середине XIX века американские газеты начали печатать шахматные задачи. Одним из первых, и к тому же самым молодым из изобретателей таких задач был ньюйоркец Сэм Лойд. В возрасте всего 14 лет опубликовал свою первую задачку в местной газете. В 17 лет он был уже одним из наиболее успешных и известных изобретателей шахматных задач в Соединенных Штатах. От шахмат Лойд перешел к математическим головоломкам и к концу столетия стал первым в мире профессиональным составителем головоломок и импресарио. Он часто публиковался в американских изданиях и утверждал, что получал от читателей до 100 000 писем в день. Эту цифру, впрочем, следует воспринимать с известной долей скептицизма. Лойд призывал людей относиться к истине как к некой забавной игре — что можно ждать от профессионального загадочника! Для начала Ллойд заявил, что именно он изобрел игру в пятнашки, и ему поверили! И только в 2006 году, когда историки Джерри Слонам и Дик Соннвелд проследили происхождение этой игры, выяснилось, что на самом деле ее придумал Ной Чепмэн. Лойд также возродил интерес к танграмам, опубликовав «Восьмую книгу о тан, Часть I», якобы являвшуюся вариантом древнего текста, посвященного 4000-летней истории этой головоломки. Книга оказалась мистификацией, хотя сначала ее всерьез восприняли даже ученые.

Лойд обладал феноменальной способностью к превращению математических задач в забавные, ярко иллюстрированные головоломки. Самой гениальной из них была головоломка, изобретенная Лойдом в 1896 году для газеты «Brooklyn Daily Eagle». Эта головоломка, называвшаяся «Таинственное исчезновение с Земли», приобрела такую популярность, что позднее ее идеей воспользовались в качестве рекламных приемов несколько известных брендов, таких как «The Young Ladies Ноше Journal» и «Большая Атлантическая & Тихоокеанская чайная компания»; кроме того, ее использовали республиканцы для своей политической программы на президентских выборах 1896 года (хотя содержащееся в ней послание вовсе не походило на политический манифест). На этой головоломке изображены китайские воины, расположенные вокруг Земли, нарисованной на картонном круге, который может вращаться вокруг своего центра [43] Круг прикреплен в центре к картонному квадрату, относительно которого и рассматриваются вращения. ( Примеч. перев. ) . Когда нарисованная на круге стрелка указывает на северо-восток, на картинке нарисовано 13 воинов, но стоит повернуть круг так, чтобы стрелка указывала на северо-запад, как один из них исчезает, и воинов остается только 12. Эта головоломка сбивает с толка. Только что перед вами было 13 воинов, а через секунду — уже только 12. Кто именно исчез и куда он делся?

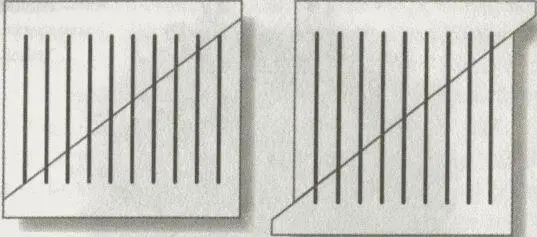
Фокус, используемый в данной головоломке, известен как геометрическое исчезновение. Его можно продемонстрировать и так: на рисунке изображен лист бумаги с нанесенными на него десятью вертикальными отрезками. При разрезании листа по диагонали получаются два куска, которые можно сложить по-другому — так, что получится только девять отрезков. Куда делся десятый? А происходит следующее: отрезки сложились таким образом, что их получилось девять, но они оказались длиннее первоначальных. Если отрезки на первом рисунке имели длину 10 единиц, то на втором их длина равна 11 1/ 9, поскольку один из исходных отрезков распределился среди девяти остальных.