Донелла Медоуз - Пределы роста. 30 лет спустя

эпидемии или социальные потрясения могут приводить к появлению на графиках зубцов, небольших подъемов или понижений, но в целом экспоненциальный рост определяет общее поведение социально-экономической системы человечества со времен промышленной революции.

Этот вид роста имеет удивительные характеристики, из-за которых им чрезвычайно трудно управлять. Поэтому перед тем, как проанализировать долговременные перспективы развития мира, дадим определение экспоненциального роста, опишем его причины и обсудим факторы, определяющие его развитие во времени. Физический рост на ограниченной планете не может продолжаться бесконечно. Вопрос в том, когда он закончится и какие силы заставят его остановиться? При каких условиях человечество и глобальная экосистема переживут его окончание? Чтобы ответить на эти вопросы, необходимо понять структуру системы, которая заставляет численность населения и капитал постоянно стремиться к росту. Эта структура лежит в основе модели World3 и, как мы считаем, именно она определяет поведение мирового общества.

Математические основы экспоненциального роста

Возьмите салфетку или бумажное полотенце и сложите его пополам. Вы удвоили его толщину. Сложите его пополам еще раз. Первоначальная толщина увеличилась в четыре раза. Снова, в четвертый раз сложите его вдвое, и оно станет в 16 раз толще, чем было сначала. Его толщина составит около сантиметра.

Если сложить его вдвое еще 29 раз, то есть всего 33 раза, какова будет его толщина? Полметра? Метр? От 1 до 10 м? От 10 м до километра?

Конечно, вы физически не сможете вдвое сложить салфетку или бумажное полотенце 33 раза. Но если бы смогли, то итоговая толщина была бы больше 5400 км — больше, чем от Москвы до Байкала [16].

Эго и есть экспоненциальный рост: удвоение, повторное удвоение и снова удвоение и т. д. Он примечателен тем, что способен достигать огромных значений за короткое время. Экспоненциально растущие параметры озадачивают нас, так как большинство людей воспринимает рост как линейный процесс. Величина растет линейно, если за постоянный период времени она возрастает на постоянную величину. Если бригада дорожных строителей каждую неделю укладывает один километр автомобильной дороги, то ее длина растет линейно. Если ребенок ежегодно кладет в копилку 7 долларов, то его сбережения увеличиваются линейно. Количество асфальта, укладываемого каждую неделю, не зависит от того, сколько уже было уложено к этому времени, и добавленная ребенком сумма тоже не зависит от того, сколько денег уже было к тому времени в копилке. Когда параметр растет линейно, приращение за

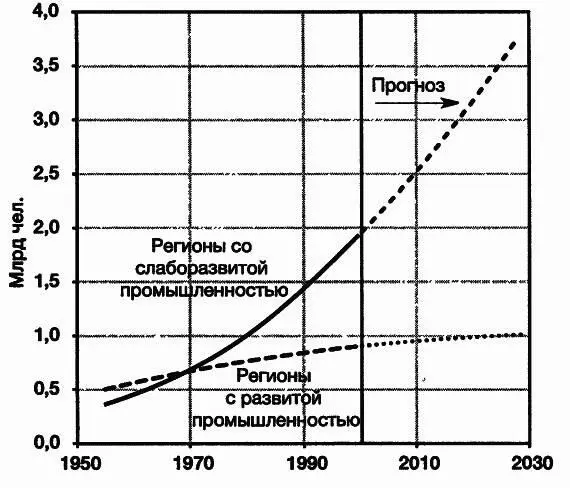
Рис. 2.2.Городское население в мире

За прошедшие 50 лет городское население экспоненциально увеличивалось в странах со слаборазвитой промышленностью и практически линейно — в промышленно развитых странах. Среднее время удвоения городского населения в странах со слаборазвитой промышленностью составляет 19 лет. Предполагается, что этот показатель сохранится в ближайшие несколько десятилетий. (Источник: UN.)

постоянный период времени всегда одинаково, оно не зависит от того, каким было само значение параметра в этот момент.

Величина растет экспоненциально, если приращение пропорционально самой величине. Колония дрожжей, в которой каждая клетка делится на две каждые 10 минут, растет экспоненциально. Из каждой клетки через 10 минут будет уже 2 клетки. Еще через 10 минут их будет уже 4, еще через 10 минут — 8, затем 16 и т. д. Чем больше клеток, тем больше новых клеток образуется в единицу времени. Прибыль компании, которая успешно увеличивает валовую выручку на определенный процент в год, через несколько лет экспоненциально вырастет. Когда параметр растет экспоненциально, приращение тоже растет с течением времени, оно зависит от того, каково значение самого параметра в этот момент.

Ключевое отличие экспоненциального роста от линейного можно проиллюстрировать на примере. Допустим, у вас есть 100 долларов. Вы можете положить деньги в банк и получать проценты (вклад с капитализацией процентов) или положить их в копилку и каждый год добавлять определенную сумму. Если вы внесли на счет 100 долларов под 7 % годовых с капитализацией, то есть добавлением процентов к сумме счета, то вклад будет расти экспоненциально. Каждый год сумма будет прирастать