Юрий Мизун - Полярные сияния

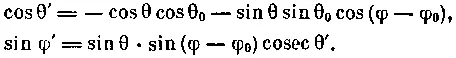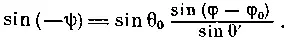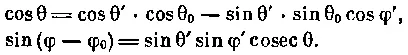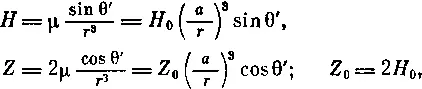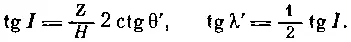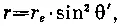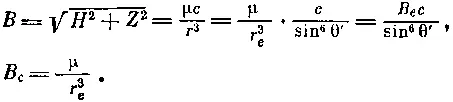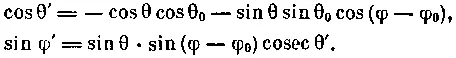
Магнитное склонение дипольного поля Ψ — это угол, образованный магнитным и географическим меридианами в точке Р . Он определяется из выражения

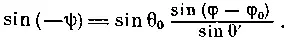
Существуют таблицы, которые содержат геомагнитные координаты сетки точек, расположенных через ровные угловые интервалы в географических координатах θ и φ. Имеются также сетки географических и геомагнитных координат. По этим сеткам можно легко найти геомагнитные координаты любой точки с известными географическими координатами, и наоборот.

Обратный переход от геомагнитных координат к географическим можно произвести по формулам

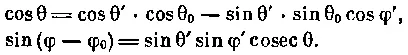
Если рассматривать только дипольную часть геомагнитного поля в любой точке Р с геомагнитными координатами θ' и φ', то потенциал V 1, описываемый членами первого порядка, равен V 1= — μ*cos θ / r 2Так как V 1не зависит от долготы, то восточная компонента дипольного поля В равна нулю. Северная Н и вертикальная Z составляющие поля получаются равными

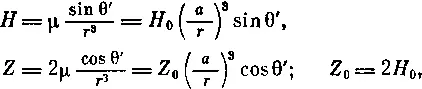
где Z 0и Н 0 — максимальные значения Z и Н на геоцентрической сфере радиуса α, содержащей точку Р. Н 0 соответствует полю на геомагнитном экваторе, a Z 0— на северном полюсе. На южном полюсе Z = —Z 0.

Наклонение I и магнитную широту λ' можно определить из следующих уравнений:

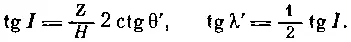
Каждая силовая линия дипольного поля лежит в плоскости геомагнитного меридиана. Ее уравнение

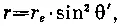
где r e— радиальное расстояние, на котором данная силовая линия пересекает плоскость геомагнитного экватора, с величиной поля равной μ / r e 3. Величину r eможно принять за параметр, определяющий силовую линию.

Напряженность поля в точке Р можно определить через параметр силовой линии

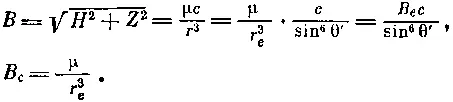
Представление геомагнитного поля центральным диполем только лишь первое весьма грубое приближение. Используя более высокие члены разложения по сферическим гармоникам, можно построить геомагнитную систему координат, лучшую, чем дипольная. Так, если использовать наряду с дипольными еще пять старших сферических гармонических членов и рассчитать геометрическое место точек пересечения земной поверхности силовыми линиями, которые располагаются в экваториальной плоскости на расстоянии пяти-шести радиусов Земли, то полученная таким образом линия хорошо совпадает с зоной полярных сияний.

Было также показано, что если проектировать по силовым линиям на поверхность Земли лежащие в плоскости экватора геоцентрические окружности с радиусами L c= α cosec 2θ c, то полученные таким путем широты θ cупорядочивают явления в полярной шапке лучше, чем дипольные геомагнитные широты.

Часто используют «исправленные» геомагнитные координаты при описании различных авроральных явлений и поглощения космического радиоизлучения в полярной шапке. Они были рассчитаны Хакурой на основе исследований Халтквиста. Дальнейшее усовершенствование этих «исправленных» геомагнитных координат выполнил Густавсон, использовав коэффициенты разложения поля на эпоху 1965 г.

При объяснении некоторых явлений, которые связаны с суточными вариациями полярных сияний, было введено понятие геомагнитных полуночи и полудня. Затем появилось и более общее понятие геомагнитного времени.

Если данная точка определена географическими координатами θ и φ и геомагнитными координатами θ' и φ', то геомагнитное время может быть выражено соотношением 15° t' = φ H' — φ'. Здесь φ' н— геомагнитная долгота полудня в данный момент времени. Геомагнитное время t' отсчитывается от геомагнитного полудня и относительно истинного положения Солнца H.

Используя схему определения «геомагнитного времени» в системе геомагнитных координат (рис. 9), приведем пример его расчета. Если в Гринвиче истинное время t G, в точке Р местное истинное время составит t G+ φ/15°, то географическая долгота истинного положения Солнца будет 180°—15° t G. Отсюда, учитывая также полярный угол этого положения (который определяется как 90°—δ, где δ обозначает склонение Солнца), геомагнитную долготу φ H' можно рассчитать по приведенным выше формулам. Гринвичское среднее время в этот момент будет t c—e , где е обозначает «уравнение времени».