Эрик Грейн - Трилогия ума - Научите ребенка думать по-новому. Восхождение от рассудочного мышления к разуму и мудрости

Учитель объясняет, что такое год – это то время, за какое Земля облетает один раз вокруг Солнца. Он длится 365 дней. Далее объясняет, что год делится на четыре ортогональных сезона и называет их: зима, весна, лето, осень. Объясняет, что такое месяц и сколько месяцев в году (12). Просит детей их назвать. Объясняет, что такое сутки – это время, за которое Земля совершает один полный оборот вокруг своей оси (за 24 часа). Как нечто целое сутки, опять-таки, делятся на четыре одинаковые по времени части. И все это учитель связывает с понятием «ортогональное» Гераклита для того, чтобы эту систему ритмов приложить к другим природным и социальным системам.

По этой теме также можно организовать игру «Назовите слова, ортогональные по значению». Учитель говорит: «День и Ночь». Ученики называют слова, ортогональные по значению: «Вечер и Утро». Учитель называет: «Зима и Лето» – ученики называют: «Весна и Осень».

Выходит, что зима, весна, лето и осень, так же как и ночь, утро, день и вечер связаны не только противоположными, но и более сложными ортогональными отношениями. Учитель просит кого-либо из учеников нарисовать Ортогональное Гераклита, и вписать в эту геометрическую модель времена года. То же самое учитель предлагает проделать детям и со временами суток. Дети должны четко знать, что день и ночь по отношению к утру и вечеру ортогональны, также как зима и лето ортогональны по отношению к весне и осени. Для демонстрации этой мысли, учитель вычерчивает на доске соотношение двух ритмов: суточного и сезонного.

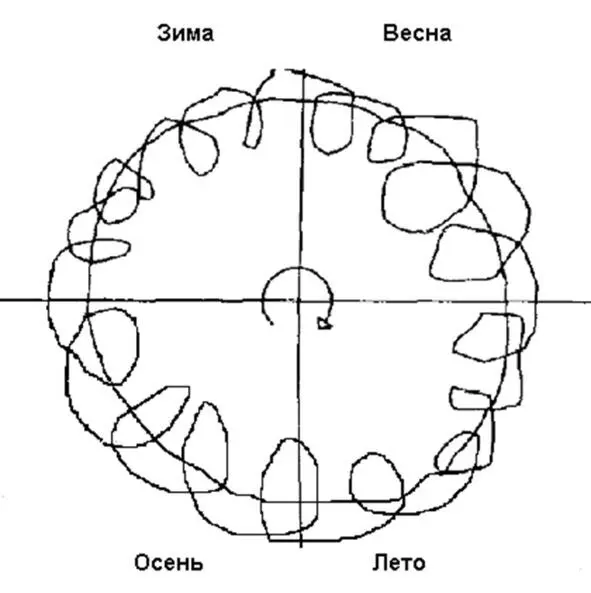
Рис. 5. Участие земли в суточных и сезонных ритмах

В старших классах, дети должны учиться понимать, что ортогональными отношениями связаны между собой север и юг с востоком и западом, потенциальная с кинетической энергией, электрическая энергия – с магнитной энергией. То же самое касается и общественных процессов, в которых рабовладельческая общественно-экономическая формация с ее противоположными классами рабов и рабовладельцев ортогональна по отношению к феодальной формации с преобладающими в ней классами феодалов и крепостных. В таком же ортогональном отношении находится старшее и младшее поколения людей, в котором папа и мама оказываются ортогональными по отношению к сыну и дочери.

Выходит, что «отцы и дети» – это не противоположные друг к другу понятия, как принято многими считать, а ортогональные. Поэтому все круговые, циклические движения во многих случаях лучше всего объяснять не при помощи пифагорейской, а при помощи гераклитовской модели, отражающей в разумном мышлении все формы обмена ресурсами. Эта же мыслительная структура напрямую касается и «клеточки» буржуазного общества, которую Карл Маркс положил в основу своего фундаментального труда «Капитал», в котором стремился переосмыслить и изменить современное ему общество с позиций разумного мышления. И совсем другое дело, удалось ли ему это.

Спрашивается, разделил ли Маркс рассудок и разум в своих трудах, как это мы проделали в представляемой читателю работе. К сожалению, не разделил. Не отделил он и мудрость от двух предшествующих ступеней в развитии ума, хотя был чрезвычайно близок к этому. В. И. Ленин, один из выдающихся вождей пролетариата где-то в своих многочисленных работах отметил: «Маркс не оставил Логики с большой буквы, но он оставил Логику «Капитала». И в этом отношении Ленин был прав. Я же скажу, что понять марксизм во всем его противоречивом многообразии, и особенно мышление самого К. Маркса можно не иначе, как овладев разумом и мудростью, как мышлением сравнительными понятиями, освоить которое мы и предлагаем в данной книге.

В методике формирования философских представлений, как мы уже видим, важное место занимает абстрагирование, т.е. движение от «вещей» к общим понятиям. Последние часто совпадают с геометрическими фигурами: прямоугольным треугольником, окружностью и т. д. А также, наоборот – от образа фигуры, от абстракции к реальным вещам и процессам. Это достигается систематическим использованием приёма материализации геометрических образов, которые зачастую адекватно отражают философские обобщения.

Не случайно при входе в Академию Платона было написано:

«Да не войдет сюда тот, кто не знает геометрии».

Ибо геометрия – это не только раздел математики, это фундаментальный элемент философской культуры, помогающий отвлекаться учащимся от конкретных свойств материальных вещей и таким образом овладевать философскими и математическими (геометрическими) знаниями и представлениями. Осмыслив первоначала и научившись при помощи них думать, школьники с помощью задаваемых учителем вопросов самостоятельно будет находить их проявления в бесконечном многообразии окружающей реальности.