Филип Тетлок - Думай медленно — предсказывай точно. Искусство и наука предвидеть опасность

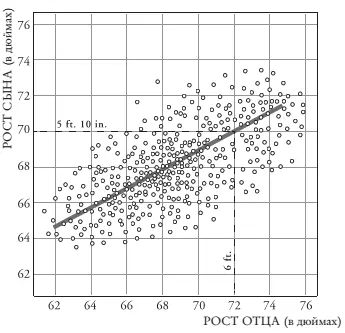
Лучшее предположение о росте сына, исходя из роста отца, предполагающее корреляцию 0,5 между двумя переменными

Если же вы будете постоянно держать в голове регрессию к среднему значению, она может стать ценным инструментом. Представьте, что у нас есть 2800 добровольцев, которые второй раз предсказывают исход 104 подбрасываний монетки. Распределение опять будет выглядеть как гауссова кривая с большинством людей в районе 50 % и крошечным количеством, которые правильно предскажут почти все или почти ничего. Но кто на этот раз покажет изумительные результаты? Скорее всего, другие люди. Корреляция между раундами будет близка к нулю, и лучшее предсказание по поводу успеха любого прогнозиста будет в районе 50 % — другими словами, произойдет тотальная регрессия к среднему значению.

Чтобы доказать это безошибочно, представьте, что мы попросим только тех, кто показал изумительно хорошие результаты в первом раунде, повторить упражнение. Благодаря регрессии к среднему значению очень вероятно, что большинство во второй раз покажут результат хуже. И ухудшение будет самым большим у тех, кому в первом раунде больше всего повезло. Угадавшие в первый раз 90 % могут резко понизить свой успех, до 50 %. Конечно, есть вероятность, что несколько человек и во второй раз покажут выдающийся результат, но тот факт, что остальные быстро регрессируют к среднему значению, заставит нас задуматься, прежде чем мы объявим их гуру подбрасывания монеток. Пусть они выполнят это упражнение снова. Рано или поздно удача от них отвернется.

Таким образом, регрессия к среднему значению — незаменимый инструмент в тестировании степени удачи в показателях: Мобуссин отмечает, что медленная регрессия чаще наблюдается в деятельности, в которой доминирует мастерство, быстрая же больше ассоциируется со случайностью [77].

Чтобы проиллюстрировать это утверждение, давайте представим себе двух людей, участвующих в турнире IARPA , — Фрэнка и Нэнси (см. график). В течение первого года Фрэнк выдавал ужасные результаты, а Нэнси — выдающиеся. На гауссовой кривой внизу Фрэнк помечен нижним показателем 1 %, а Нэнси — верхним показателем 99 %. Если их результаты были вызваны исключительно удачей — как с подбрасыванием монетки, — в течение второго года мы можем ожидать, что Фрэнк и Нэнси регрессируют к среднему значению, т. е. к 50 %. Если их результаты были в равных долях обусловлены мастерством и удачей, мы можем ожидать половинчатую регрессию: Фрэнк поднимется примерно до 25 % (между 1 и 50 %), а Нэнси опустится до 75 % (между 50 и 100 %). Если же их результаты полностью зависели от мастерства, не будет никакой регрессии: Фрэнк проявит себя так же ужасно в течение второго года, а Нэнси будет все так же блистать.

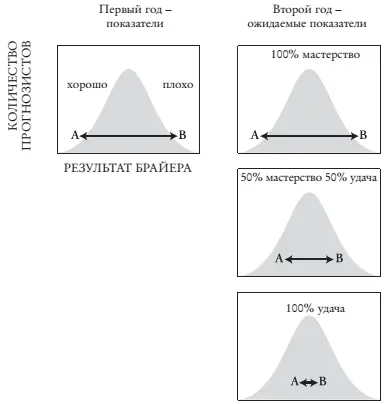
Степень удачи в турнире определяет степень регрессии к среднему значению от одного года к другому

Так и какие же результаты получились у суперпрогнозистов за несколько лет? Это ключевой вопрос. И ответ на него — феноменально хорошие. Например, за второй и третий год мы увидели процесс, обратный регрессии к среднему значению: суперпрогнозисты в общем и целом, включая Дага Лорча, на самом деле увеличили свой отрыв от других прогнозистов.

Но этот результат должен вызвать подозрение у внимательных читателей. Он означает, что за результатами суперпрогнозистов стоит совсем мало удачи — или ее и вовсе нет. А учитывая то, что они предсказывали — и редкую неопределенность, которая кроется в некоторых вопросах, — я сильно в этом сомневаюсь. Некоторые ситуации разрешились в последний момент благодаря внезапным событиям, которые никто с этой стороны от Господа не способен был предугадать. В частности, задавали вопрос на тему, произойдет ли фатальное столкновение судов в Восточно-Китайском море. Ответ оказался утвердительным, причем произошло это в последний момент перед окончанием срока, на который задавался вопрос, когда разозленный капитан рыболовецкого судна пырнул ножом южнокорейского офицера прибрежной охраны, конфисковавшего его судно за нарушение границы. Другие вопросы покоятся на сложных взаимодействиях между системами переменных. Возьмите, к примеру, вопрос о цене на нефть, который давно уже считается могилой для репутаций прогнозистов [78]. Количество факторов, которые могут как повысить цену на нефть, так и понизить ее, огромно: от действий нефтяников в США до действий джихадистов в Ливии и производителей батарей в Силиконовой долине. А количество переменных, которые могут повлиять на указанные факторы, еще больше. Многие из этих случайных связей еще и нелинейные — что, как показал Эдвард Лоренц, означает, что даже такое крошечное действие, как взмах крыльями бабочки, может иметь драматические последствия.