Кэролайн Уилльямс - Мой продуктивный мозг [Как я проверила на себе лучшие методики саморазвития и что из этого вышло]

Помню, когда я проходила тест с Бетти, мне казалось невозможным поменять свое решение, если рука уже потянулась к какой-то кнопке. Теперь же нет ничего проще. Вряд ли это случайность: ведь почти все, чем я занималась с тех пор, было направлено на развитие функций префронтального контроля головного мозга. И то, как я справилась с заданием с роботами, по-видимому, доказывает, что определенного успеха на этом пути я добилась. А может быть, все дело в стимуляции, которую я в тот день получала через очаровательную резиновую шапочку. Позже я узнала, что за всем, что происходило со мной в тот день, стоит следующая теория: развитие оперативной памяти «переходит в распоряжение» навыку, для которого она в данный момент нужна (например, навыку решения арифметических примеров). Получается, мы снова вернулись к тренировке оперативной памяти, хоть и в формате более интересной игры. Наверное, уже можно не удивляться. Я рассказала Амару, как постоянно сталкивалась с управляющими функциями мозга на своем пути. «Бóльшая часть вашей книги — это и есть управляющие функции», — подтвердил он.

После этого у меня выдался целый свободный вечер в Оксфорде, так что я направилась в один из многочисленных книжных магазинов города в надежде найти хороший справочник по математике. Амар был не в восторге от этой идеи — в эксперимент добавится еще один фактор, на который он не рассчитывал. Но так как наши изыскания все-таки не вписываются в рамки полноценного научного исследования, да и у меня будут всего две тренировочные сессии на фабрике роботов (вместо нескольких недель в полноценном исследовании), он мне уступил. Несколько минут занятий математикой в день вряд ли что-то серьезно изменят. Амар сказал, что иногда изменений не видно даже после нескольких недель тренинга, потому что у некоторых они проявляются только со временем.

Кстати, идея купить справочник посетила меня еще до поездки в Оксфорд. Но, во-первых, мне не хотелось искажать свои исходные результаты, начав тренироваться слишком рано, и, во-вторых, внесло свою лепту мое отвращение к математике. Я пошла в местный книжный магазин, направилась к стеллажу со справочниками, достала книгу по математике для подростков, открыла ее на случайной странице, и… ну, там с таким же успехом могли находиться фотографии разлагающихся трупов. Я буквально отпрянула, запихала книгу обратно на полку и буквально через мгновение уже бежала домой.

В Оксфорде я решила быть к себе добрее и выбрала справочник для подготовки выпускников четвертого курса. И тем же вечером, пока ехала на поезде повидаться с другом в близлежащем городке, я испытала свои силы: один вопрос за другим, никуда не торопясь, каждый раз сверяясь с ответами. Возможно, утренняя чистка что-то изменила в моем мозгу, и, как ни странно, мне понравилось. С каждым правильным решением моя уверенность в себе росла. Я набрала 96 % правильных ответов. Очень даже неплохо.

Через несколько недель Амар прислал результаты эксперимента, согласно которым мои математические навыки действительно улучшились. В контрольных тестах, где мне нужно было пробраться через несколько страниц с задачками на умножение, деление в столбик и т. п., до тренинга я набрала 98 баллов, а после — 106 (рис. 17). Казалось бы, незначительное улучшение — но на Амара оно произвело впечатление: «Твои результаты улучшились на 8,1 %. Это очень ощутимый результат, учитывая, что ты выполнила всего два подхода». Он сказал, что, основываясь на данных других исследований, практический эффект наблюдается уже при улучшении примерно на 2 %.

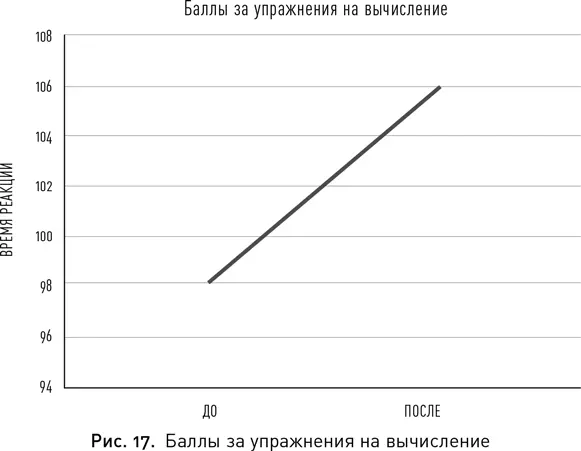
Однако Амар не уверен, что остальные 6 % как-то связаны с тренировкой: «Это всего лишь одиночное измерение, и можно найти целый ряд причин, по которым вам бы хотелось продемонстрировать улучшения в итоговых тестах». Сыграть свою роль могли и мои ожидания, и возврат к норме (странный закон статистики, в соответствии с которым полученные во второй раз баллы при любых измерениях будут ближе к среднему, чем первые, — даже вне зависимости от того, пытались вы что-то изменить или нет).

Кстати, в организации упражнений был еще один важный момент, которому я не уделила особенного внимания. Прежде чем появлялось новое уравнение, на экране вспыхивали слова с негативной или позитивной коннотацией («первичное сообщение»). В более раннем исследовании ‹‹4›› , на котором основывались эксперименты Амара, люди с высокой математической тревожностью быстрее реагировали, если первичное сообщение было негативным, например «бесполезный» или «неудача». Эти результаты удивили исследователей, ведь обычно именно позитивное мышление помогает людям работать лучше. Но получается, что при математической тревожности результаты улучшались быстрее, если первичное сообщение было созвучно их оценке собственных способностей — даже если оно было негативным.