Георгий Челпанов - О памяти и мнемонике

Он приводит в пример лицо, которое обладает поразительной памятью на числа и хронологические даты. Годы самых незначительных исторических событий или, еще лучше своей собственной жизни он может воспроизводить с такой определенностью, что иногда сам этому удивляется. Из наиболее важных событий из мировой истории, если только их можно датировать, найдутся очень немногие, в особенности военные события, года которых он не мог бы сразу определить. День рождения и смерти знаменитых личностей он обыкновенно определяет с удивительной точностью. Он мог, например, без предварительного приготовления безошибочно определить дни и годы рождения знаменитых немецких властителей, начиная от Фридриха 1 Барбароссы и кончая Людовиком Баварским, а равным образом дни знаменитейших сражений. Кроме того, он знает год и день рождения не только выдающихся властителей, но даже более или менее замечательных деятелей в области литературы и искусства, например, знаменитых ученых, музыкантов. Но что для нас всего интереснее, так это то, что он, при желании запомнить ту или другую хронологическую дату, пользуется всеми своими диаграммами. Так, если он, например, желает запомнить год, месяц, число, день и час смерти Фридриха Великого (четверг, 17 августа, 1786 г., 2 часа 20 минут утра), он припоминает диаграмму числа года, затем диаграмму для обозначения месяцев, затем диаграмму для обозначения дней недели, часов дня и т.д. Следовательно, несомненно, что пользование этими диаграммами имеет мнемотехническое значение.

И это обстоятельство делает для нас понятным, что в древности могла существовать система, которая рекомендовала запоминать те или другие данные при помощи различных изображений. Очевидно, что изобретатель и лица, пользовавшиеся этим приемом, принадлежали к зрительному типу.

Для того чтобы ближе характеризовать зрительный и слуховые типы, я позволю себе привести в пример знаменитых в настоящее время счетчиков, Диаманди и Иноди. Их называют знаменитыми счетчиками потому, что они умственно производят такие числовые операции, которые человеку с обыкновенными умственными способностями, кажется, совершенно недоступны. Я привожу в пример только этих двух, еще в настоящее время живых счетчиков потому, что они принадлежат к совершенно различным типам памяти. Их способность воспроизведения исследовал и описал французский психолог Бинэ.

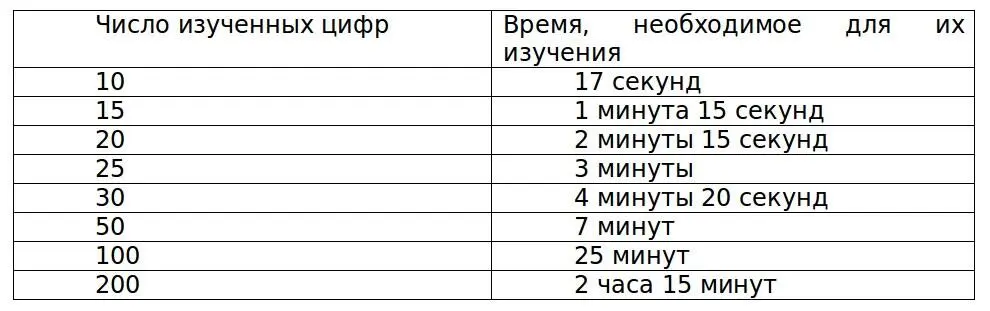
Первый из этих счетчиков, Диаманди, по происхождению грек, родился в 1868 году, на одном из Ионийских островов. Сначала готовился к коммерческой деятельности и в это время обнаружил способность к сложным умственным вычислениям. В 1893 году поехал в Париж, чтобы представиться членам Академии, и здесь-то Бинэ производил над ним свои исследования. Он может умственно производить следующие операции счисления. Он может запомнить ряды цифр с изумительной скоростью. Бинэ измерил то количество времени, которое ему нужно для того, чтобы запомнить числа, состоящие из 10, 15 цифр и т.п. Вот таблица, показывающая время, необходимое для изучения этих чисел:

Он может производить умножение многозначных чисел на многозначные, например, 5-тизначное на 5-тизначное. В течение 4 минут 35 секунд он произвел умножение 39 257 х 870 326 = 3 428 156 782.

Умножение он производил при помощи следующего приема.

Положим, ему нужно умножить 46 273 на 729. Он тотчас начинает писать общее произведение, начиная справа налево.

Когда мы производим умножение письменно, то мы это делаем таким образом, что сначала находим первое частное произведение, умножив 46 273 на 9, затем находим второе частное произведение, умножив на 2 и т.д. Затем складываем все частные произведения. Диаманди поступает иначе. Он умножает 3 на 9 и сразу в общем произведении пишет 7. а в уме держит 2, затем помножает 9 на 7 = 63, прибавляет 2, получает 65, он умственно пишет в частном произведении 5, а в уме держит 6. Затем начинает умножать на второе число множителя, т.е. на 2; он умножает 2 на 3, получает 6, к 6 он прибавляет 5, получает 11, он единицу пишет в общем произведении. Следовательно, его прием умножения состоит в том, что вместо того, чтобы получить все три частных произведения, он вычисляет в отдельности цифры частных произведений, находящихся в одном столбце, чтобы, сложив их, получить цифру общего произведения. Таким образом, он получает сначала цифру общего произведения 7, затем 5 и затем 6, которые он складывает, что дает в общем произведении 1; затем 4, 4, 1, складывая которые вместе с удерживаемым в уме, он получает в общем произведении 0. Очевидно, что такой прием для Диаманди более легок, чем нахождение частных произведений.