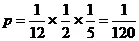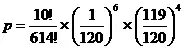Леонид Васильев - Внушение на расстоянии

Ведущие современные парапсихологи (д-р Райн, проф. Соул и др.) не считают, однако, даже и такие наблюдения достаточным доказательством реальности телепатической связи. Неоспоримыми они считают только экспериментальные данные, получаемые с применением количественных методов изучения мысленного внушения. С этим мнением нельзя не согласиться.

К рассмотрению таких методов и получаемых с их помощью результатов мы теперь и перейдём.

Впервые применённые (как уже было сказано в первой главе) Шарлем Рише количественные экспериментальные методы получили дальнейшее развитие в 30-е годы текущего столетия. В 1927 г. американский профессор В. Мак Дугалл (Mc.Dougall) обратился к учёному миру с призывом содействовать развитию парапсихологии. На этот призыв среди других учёных отозвался молодой в то время биолог Райн (J. B.Rhine) — один из основателей современных количественных исследований в парапсихологии. В Англии тогда же вступил на этот путь Соул (S.G. Soal), ныне профессор математики в Лондонском университете. Сперва он пришёл к заключению, что, удача в телепатических опытах основана на простой случайности; но, проведя огромное число таких опытов, он изменил своё мнение и стал убеждённым защитником реальности мысленного внушения. Последователи Шарля Рише появились в те же годы и во Франции — на родине знаменитого физиолога. Один из них, Дезуаль, считал возможным успешно применять теорию вероятностей даже при небольшом числе опытов мысленного внушения.

Предоставим слово самому Дезуалю и посмотрим, как он ставил свои опыты и как применял к ним теорию вероятностей [34] R. Desoille. De quelques conditions auxquelles il faut satisfaire pour reussir des experiences de Telepathie provoquee. «Revue Metapsychique», 1932, № 6. .

«Я предупредил испытуемого о том, что буду мысленно внушать ему изображение одного из французских денежных знаков, и приступил к внушению; испытуемый объявил: „Это десятифранковый билет“, что было правильно. Я спросил его, видит ли он билет в прямом положении или перевёрнутым, и испытуемый ответил правильно: „Перевёрнутым“. Наконец, я задал ему ещё один вопрос: „В каком состоянии находятся уголки билета?“ и снова получил правильный ответ: „Верхний левый угол загнулся“. Внушаемый образ был воспринят во всех подробностях».

Подсчитаем теперь вероятность этого результата, предположив, что он был получен вследствие случайной удачи. При внушении французских денежных знаков число возможных случаев равно 12 (монеты в 1, 2, 5, 10 су и в 1, 2 франка; кредитные билеты стоимостью в 5, 10, 50, 100, 500 и 1000 франков). Вероятность совпадения в этом случае равняется 1/12; для угадывания перевернутого положения билета вероятность равна 1/2; и для правильного указания на загнутость одного из углов вероятность равна 1/5 (отсутствие загнутости и один загнутый угол из четырёх составляют 5 возможных случаев). Полная вероятность равняется:

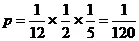
Если я поставил 10 таких опытов (причём каждому из них соответствует вероятность 1/120) и если ответы оказались правильными в 6 опытах из 10 (что можно получить с хорошим перципиентом довольно легко), то вероятность совпадений, основанная на случайной удаче, выразится так:

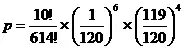
что приближённо будет [35] Приведенное рассуждение основывается на положениях теории вероятностей — ветви математики, изучающей случайные явления. Читатель может ознакомиться с ней по книгам (в порядке возрастающей трудности): О.Яхот. Необходимость и случайность. М., Госполитиздат, 1956; Э.Борель. Вероятность и достоверность. М.,Физматгиз,1961; Б.В.Гнеденко и А.Я.Хинчин. Элементарное введение в теорию вероятностей, изд. 4-е. М. — Л., Гостехиздат, 1957. Вероятностью случайного события (= Р) называется отношение числа благоприятных шансов к общему числу равновозможных взаимоисключающих шансов. Вероятность сложного события равняется произведению вероятностей частных событий. При вычислении вероятностей употребляется ряд вспомогательных понятий и обозначений. В частности число, сопровождаемое восклицательным знаком, которое называется «факториал» и означает: n! = 1 x 2 x 3 x… x n (см. М.Я.Выгодский. Справочник по элементарной математике, изд. 10, М., Гостехиздат, 1957, стр. 243). Очень большие и очень малые числа часто изображаются в виде числа, помноженного на 10, возведенное в ту или иную степень. При этом: 10 3 = 1000, 10 2 = 100, 10 1 = 10, 10° = 1, 10 -1 = 0,1, 10 -2 = 0,01… 10 -12 = 0,000000000001 (см. М. Я. Выгодский; цит. соч., стр. 221–222). :