Владимир Сурдин - Солнечная система (Астрономия и астрофизика)

На рис.11 изображена более замысловатая периодическая орбита, показывающая их богатое разнообразие. КА на такой орбите попеременно является то спутником Земли, то спутником Луны.

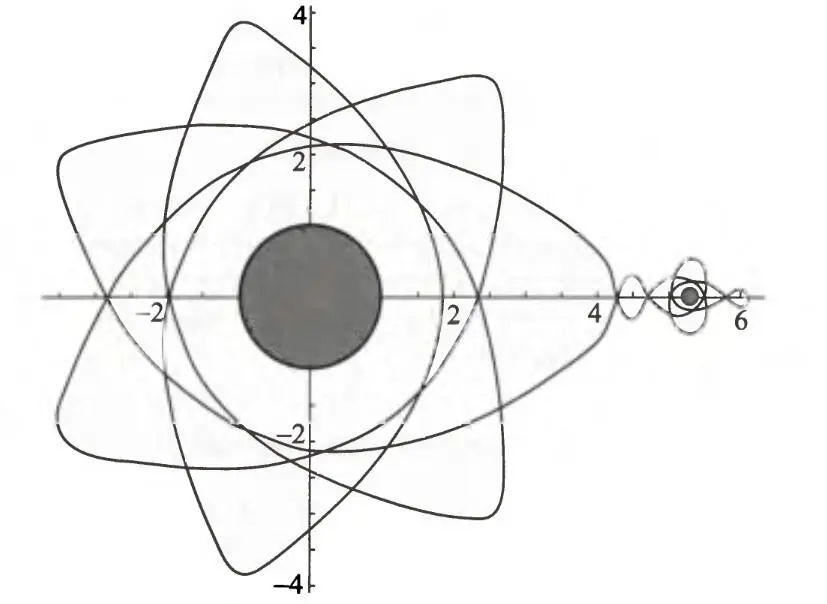
Рис.11

Задача о движении КА в гравитационном поле Земли и Солнца математически тождественна задаче о движении в поле Земли и Луны. Тут тоже существуют периодические орбиты и точки либрации. Более того, они уже используются на практике. Космический аппарат SOHO для исследования процессов на Солнце находится все время на гало-орбите вблизи точки L 1 .

Решения задачи о движении объекта в окрестности двух массивных тел оказывается очень полезным, и не только в приложении к Солнечной системе: они используются и при изучении движения вещества в двойных звездных системах, и в звездных скоплениях, и в системах галактик. Но нужно помнить, что все эти полезные решения получены при определенных предположениях. Например, точки Лагранжа существуют в рамках ограниченной задачи: два тела имеют конечные массы (любые; обе массы могут быть даже равны друг другу), а третья бесконечно мала (у нас это космический аппарат). Движение в окрестности коллинеарных точек либрации L 1 , L 2 , L 3 всегда неустойчиво. Устойчивость движения в окрестности треугольных точек Лагранжа L 4 , L 5 зависит от соотношения между массами основных тел. Обозначим массы основных тел через m 1≥m 2 . Введем безразмерный параметр µ , выражающий отношение этих масс:

µ=m 2/(m 1+m 2)

А.М. Ляпунов доказал, что движение в окрестности треугольных точек либрации устойчиво в первом приближении при 27µ(1—µ)<1 , что равносильно условию

µ<���µ 0=0,0385209 .

Для системы Земля-Луна µ<(1/3)/µ 0 , значит, треугольные точки либрации устойчивы (при отсутствии не учтенных в задаче возмущений!). А вот для системы Плутон-Харон µ>3,7µ 0. Устойчивости нет. В системах двойных звезд, как правило, µ>µ 0 и движение неустойчиво.

Итак, у нас в запасе внушительный набор орбит, по которым можно двигаться долго-долго, не затрачивая ни малейших усилий. Но как попасть туда? Будем считать, что мы уже вышли в космос на круговую орбиту искусственного спутника Земли. А теперь нам надо перейти на более высокую орбиту. Тоже круговую и лежащую в той же плоскости. Имея супер-ракету, можно перелететь с орбиты на орбиту множеством способов. Но современные ракеты пока не позволяют развивать скорости в сотни километров в секунду, так что не все способы реализуемы. А поскольку каждый лишний грамм груза на борту — все равно что кирпич в рюкзаке у туриста, из возможных способов следует выбрать оптимальный, т.е. требующий минимального количества топлива.

Реактивные двигатели работают без перерыва несколько минут, тогда как перелеты длятся часы, а межпланетные — месяцы и годы. Так что можно считать без большой ошибки, что космический корабль практически мгновенно получает добавку скорости (как говорят, к аппарату прикладывается импульс скорости). Чтобы уйти с орбиты старта, нужен по крайней мере один импульс υ 1 . Чтобы остаться на орбите финиша — еще один υ 2 . Так называемая характеристическая скорость υ 1+υ 2 , а с ней и расход топлива, будут минимальными, если импульсы прикладывать по касательным (рис.12). Это было доказано еще в 1920-е гг. В. Гоманом в Германии и Ф.А. Цандером у нас.

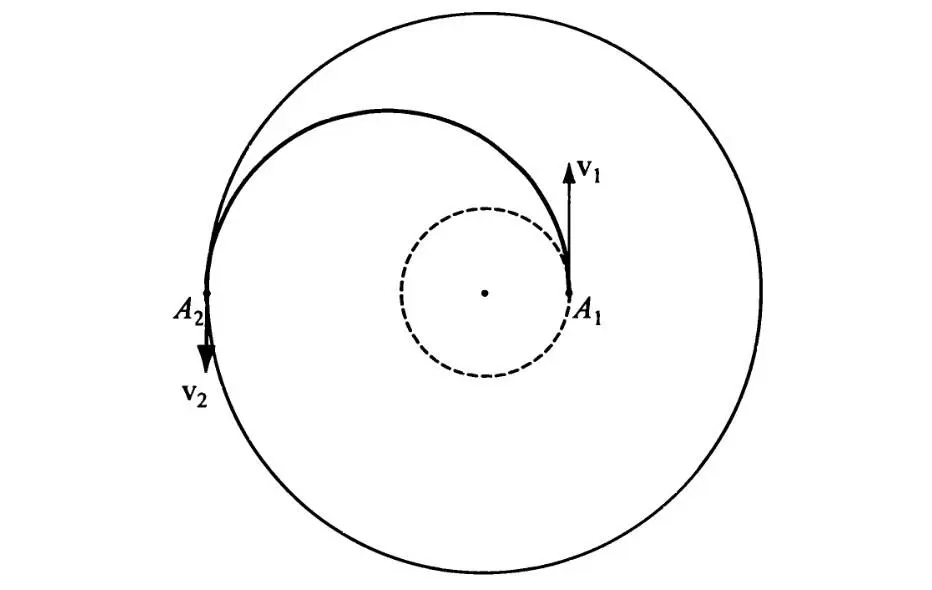
Рис.12

В космосе все движения обратимы. Точнее, если все скорости всех тел изменить на противоположные, то они будут двигаться по тем же орбитам, но в противоположную сторону. В частности, если все стрелки на рис.12 перевернуть, то получим тоже допустимые движения. Это значит, что оптимальный перелет с высокой на низкую орбиту — тот же эллипс Гомана-Цандера с теми же импульсами υ 2 и υ 1 , но на этот раз не разгонными, а тормозными, в результате чего в дальнейшем можно ограничиться перелетами на более высокие орбиты.

Отнюдь не всегда начальная и конечная орбиты лежат в одной плоскости. Существенное изменение плоскости орбиты — задача, непосильная для современных ракет (опять космический парадокс: автомобилю трудно забираться на гору, но ничего не стоит свернуть направо). Действительно, чтобы повернуть плоскость орбиты на 60°, по правилу векторного сложения скоростей требуется импульс, равный скорости движения КА, т.е. 8 км/с для низких спутников Земли.