Сравнение полученных с помощью данных выражений значений со значениями выражений (16) позволит сделать вывод о возможности решения задачи без перерасхода ресурсов. Это, со всей очевидностью, будет возможно, если одновременно выполняются соотношения (19), что означает, что движение к цели происходит не медленнее, чем запланировано, а расход ресурсов при этом происходит не быстрее, чем запланировано:
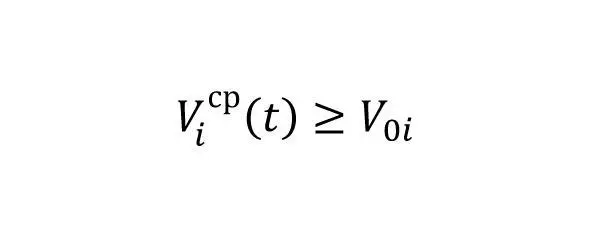
выражение 19.1
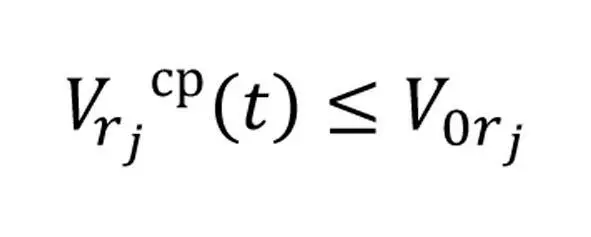
выражение 19.2
При невыполнении какого-либо условия (19) необходимо произвести коррекцию режима движения, т.е. определить среднюю скорость движения или расходования ресурса на остаточный участок движения (20):
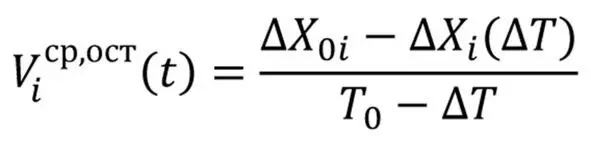
выражение 20.1
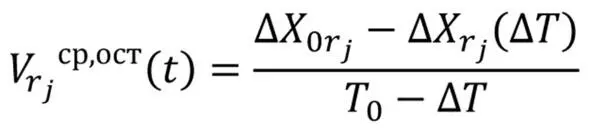
выражение 20.2
При этом, следует учитывать, что эти скоростные показатели являются взаимозависимыми, т.е. если один из них определяется выражением (20), то второй должен определяться соответствующим выражением (17).
В тех случаях, когда обеспечивается постоянный приток потребляемого ресурса (обычно извне), что позволяет не обращать внимания на ограниченность запаса, следует исходить не из зависимости между исчерпанием ресурса и скоростью перемещения в пространстве состояний (по соответствующему параметру), а из зависимости между интенсивностью потребления (поступления) ресурса и скоростью решения задачи.
Под интенсивностью I rj потребления (поступления) той или иной сущности (в данном случае того или иного ресурса) можно понимать прохождение того или иного количества указанной сущности R j в единицу времени через некоторую специально фиксированную точку, именуемую точкой потребления или точкой генерации сущности (21):
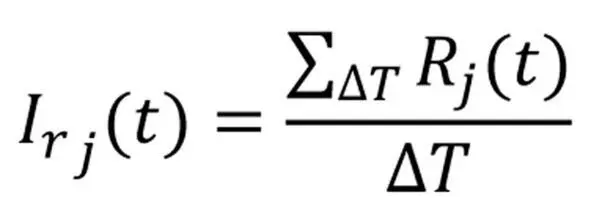
выражение 21
где числитель в дробной части выражения обозначает весь объем проходящей сущности через фиксированную точку потребления (генерации) за данный период времени (см. 8/1).
Как видно из выражения (21) интенсивность потребления (поступления) аналогична средней скорости исчерпания ресурса для локализованного фиксированного источника. В случае наличия исключительно собственного фиксированного запаса ресурса объекта интенсивность потребления (поступления) совпадает с текущей средней скоростью исчерпания ресурса.
В противном случае (наличие внешнего источника ресурса) зависимость скорости решения задачи от интенсивности может быть отображена выражениями (22):
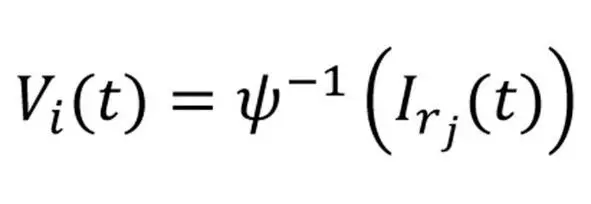
выражение 22.1
Может существовать и обратная зависимость (22.2), которая может рассматриваться как предъявление требований к потоку сущности, исходя из необходимости решения задачи:
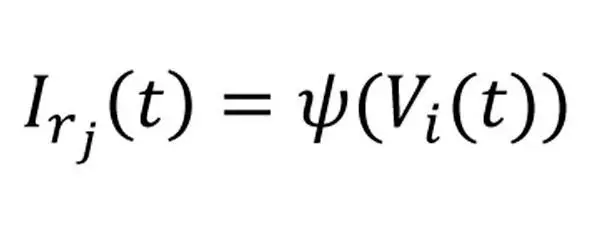
выражение 22.2
Так же, как и в случае ограниченного запаса ресурса, можно говорить о средней скорости решения задачи (выражение 16.1), о текущей средней скорости решения задачи (выражение 18.1), остаточной средней скорости решения задачи (выражение 20.1), об интенсивности (выражение 21) за период решения задачи, обозначение которого см. 8/1, об интенсивности за период решения задачи T 0 (выражение 23):
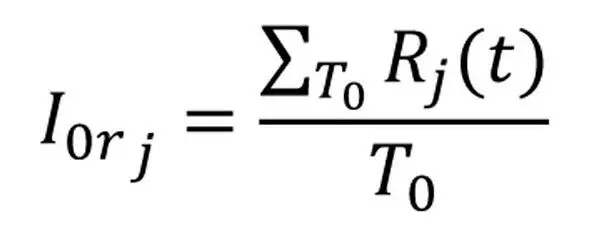
выражение 23
Если значение интенсивности получено с помощью выражения (22.2), где в качестве скорости решения задачи используется планируемая средняя скорость прохождения этапа, то выражение (23) позволяет определить объем потребляемой сущности, необходимый для полного решения задачи.
В этом случае выражение (23) можно рассматривать как норматив интенсивности потребления сущности при решении данной задачи. Не превышение его потребления в процессе решения задачи при сохранении или превышении нормативной скорости решения задачи позволяет говорить об удачной тактике прохождения этапа.
Читать дальше

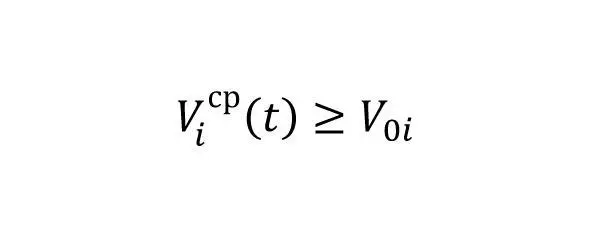
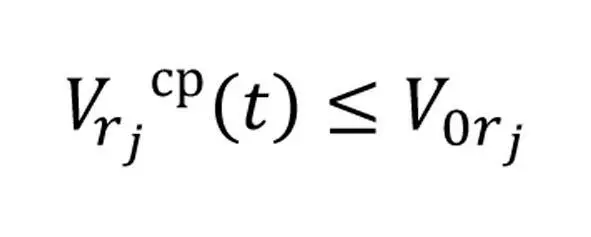
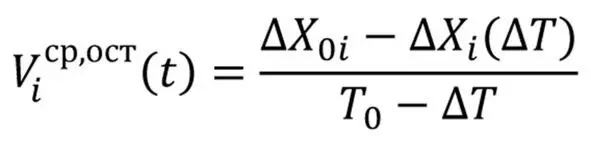
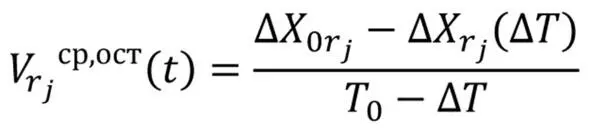
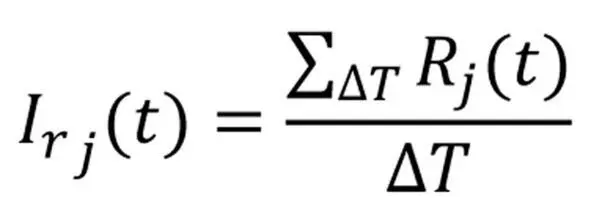
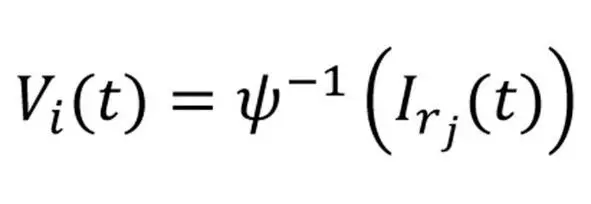
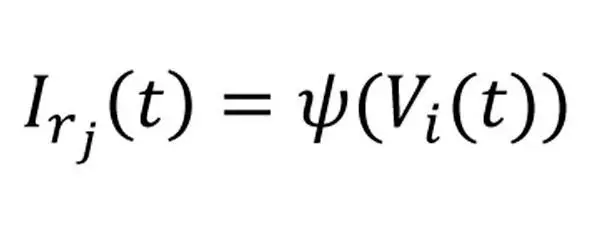
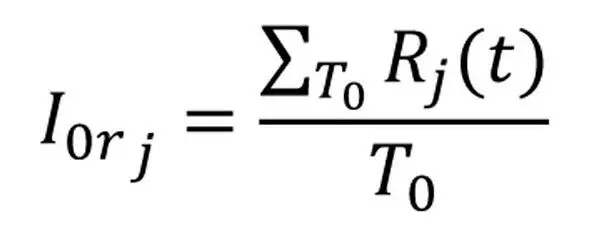






![Коллектив авторов Биографии и мемуары - Ковалиная книга. Вспоминая Юрия Коваля [второе издание, исправленное и дополненное]](/books/430445/kollektiv-avtorov-biografii-i-memuary-kovalinaya-kn-thumb.webp)



