Каниа Кан - Нейронные сети. Эволюция

Чтобы получить более полное представление о возможностях объектов, давайте добавим в наш класс переменные, которые будут хранить специфические данные этих объектов, а также методы, позволяющие просматривать и изменять эти данные:

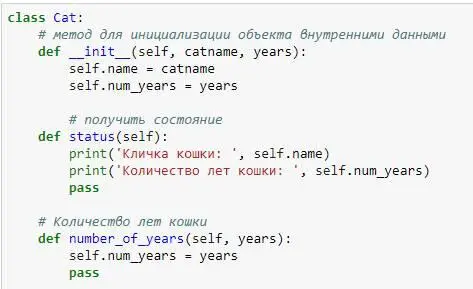
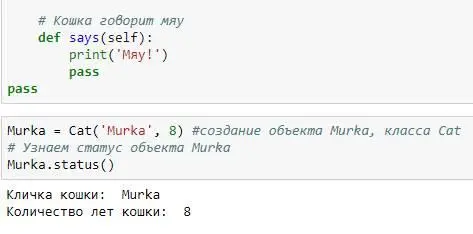
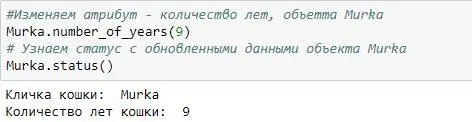
Давайте разбираться что же мы тут написали.

В любом классе можно определить функцию __init__(). Эта функция всегда вызывается, когда мы создаем реальный объект класса, с изначально заданными атрибутами. Атрибут – это переменная, которая относится к классу, в котором она определена. В нашем случае, при создании объекта, мы сразу можем указать его атрибуты – кличку и количество лет, которые сразу присваиваются этому объекту. Через созданный нами метод status(), мы можем вывести информацию о количестве лет и кличке нашего объекта. Метод number_of_years (self, years), принимает число и изменяет атрибут класса – количество лет. Метод says(), не изменился, он все также говорит голосом нашего объекта – ‘Мяу!’.

Настало время практически реализовать линейную классификацию. Для этого в Python смоделируем работу искусственного нейрона. Попробуем решить нашу задачу, найдя промежуточные значения, при заданном наборе входных и соответствующим им выходным (целевым) параметрам. Как мы помним – это были высота и длина двух разных видов животных. Это может быть и любой другой условный набор данных, которые можно представить, как параметры размеров одежды, предметов, насекомых, веса, стоимости, градусов и любых других. Отобразим наше задание – список с параметрами двух видов животных:

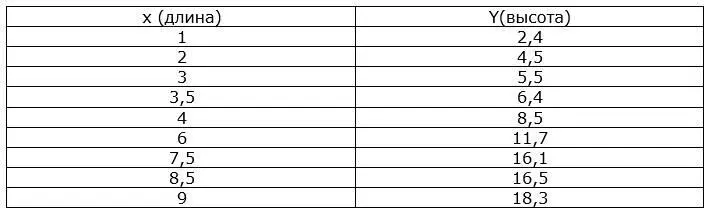
В дальнейшем все данные, которые надо анализировать при помощи искусственных нейронов и их сетей, будем называть – обучающей выборкой. А процесс изменения коэффициентов, в нашем случае – коэффициент А, в зависимости от функции ошибки на выходе, будем называть – процессом обучения.

Примем за значение х– длины животных, а Y– высота. Так как Y(игрек большое) – это и есть ответ: Y = Ax, то условимся что он и будет целевым значением для нашего нейрона (правильным ответом), а входными данными будут все значения переменной х.

Отобразим для лучшего представления входных данных, график обучающей выборки:

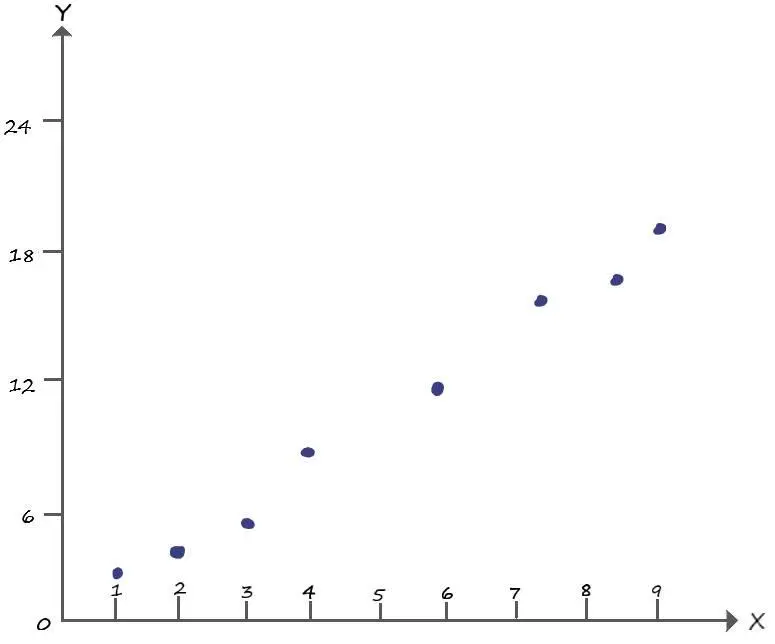
Видно, что наши данные напоминают прямую линию, уравнение которой Y = = 2* x. Данные находятся около значений этой функции, но не повторяют их. Задача нашего нейрон суметь с большой точностью провести эту прямую, несмотря на то, что данные по остальным точкам отсутствуют (например, нет данных о Yкоординате с точкой с x = 5).

Cмоделируем такую структуру, для чего подадим на вход нейрона (дендрит у биологического нейрона), значение x, и меняя коэффициент A(синапс у биологического нейрона), по правилам, которые мы вывели с линейным классификатором, будем получать выходные значения нейрона y(аксон у биологического нейрона). Так же условимся, что Y (большое) – правильный ответ (целевое значение), а y(малое) – ответ нейрона (его выход).

Визуализируем структуру нейрона, которую будем моделировать:

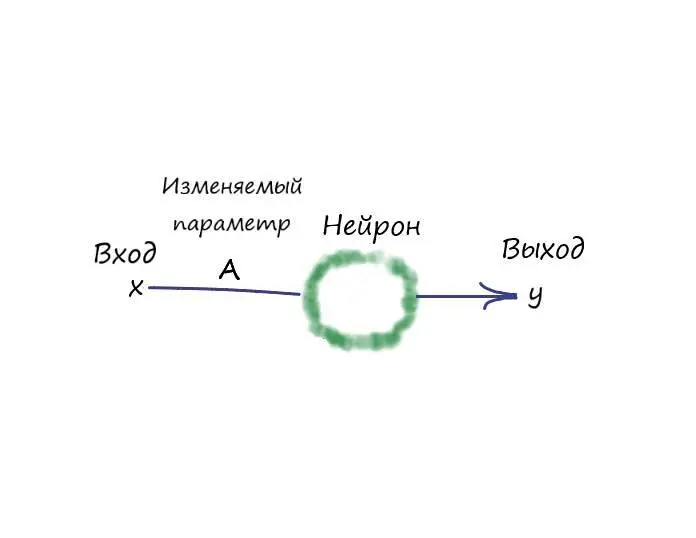
Запрограммировав в Python эту структуру, попробуем добиться прямой, которая максимально точно разделит входные параметры.

Программа

Действовать будем так же, как мы действовали, рассчитывая линейный классификатор.