Каниа Кан - Нейронные сети. Эволюция

# Функция для отображения готовой прямой

def func(x):

return [A*i for i in x]

# Значения по X входных данных

x_data = arr_x

# Значения по X начальной прямой (диапазон значений)

x_begin = [i for i in range(0, 11)]

# Значения по X готовой прямой (диапазон значений)

x = [i for i in range(0, 11)]

#x = np.arange(0,11,1)

# Значения по Y входных данных

y_data = func_data(x_data)

# Значения по Y начальной прямой

y_begin = func_begin(x_begin)

# Значения по Y готовой прямой

y = func(x)

# Зададим имена графику и числовым координатам

plt.title("Neuron")

plt.xlabel("X")

plt.ylabel("Y")

# Зададим имена входным данным и прямым

plt.plot(x,y, label='Входные данные', color = 'g')

plt.plot(x,y, label='Готовая прямая', color = 'r')

plt.plot(x,y, label='Начальная прямая', color = 'b')

plt.legend(loc=2) #loc – локация имени, 2 – справа в углу

# представляем точки данных (х,у) кружочками диаметра 10

plt.scatter(x_data, y_data, color ='g', s=10)

# Начальная прямая

plt.plot(x_begin, y_begin, 'b')

# Готовая прямая

plt.plot(x, y, 'r')

# Сетка на фоне для улучшения восприятия

plt.grid(True, linestyle='-', color='0.75')

# Показать график

plt.show()

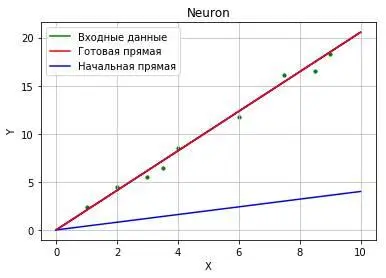
При выполнении кода, результат визуализации окажется следующим:

Исходники с программами вы можете найти по ссылке: https://github.com/CaniaCan/neuralmaster

Перед тем как описать полученный результат, сперва опишем работу нашего кода пакета matplotlib.

В функциях отображения входных данных – def func_data(x_data), def func_data(x_begin), def func_data(x), возвращаем координаты y, в соответствии со своими значениями по х.

Зададим имена графику – plt.title(), и числовым координатам – plt.xlabel():

plt.title("Neuron")

plt.xlabel("X")

plt.ylabel("Y")

Зададим имена входным данным и прямым – plt.plot(), в скобках укажем имя и цвет, plt.legend(loc=2) – определяет нахождение данных имен на плоскости:

plt.plot(x,y, label='Входные данные', color = 'g')

plt.plot(x,y, label='Готовая прямая', color = 'r')

plt.plot(x,y, label='Начальная прямая', color = 'b')

plt.legend(loc=2) #loc – локация имени, 2 – справа в углу

Метод scatter выводит на плоскость точки с заданными координатами:

plt.scatter(x_data, y_data, color ='g', s=10)

Метод plot выводит на плоскость прямую по заданным точкам:

plt.plot(x, y, 'r')

Ну и наконец отображаем все что натворили, командой plt.show().

Теперь разберем получившийся график. Синим – отмечена начальная прямая, которая изначально не выполняла никакой классификации. После обучения, значение коэффициента A, стабилизируется возле числа = 2.05. Если провести прямую функции y = Ax = 2.05*x, отмеченной красным на графике, то получим значения близкие к нашим входным данным (на графике – зеленые точки).

А что если, наш обученный нейрон смог бы правильно отвечать на вводимые пользователем данные? Если задать условие, что всё что выше красной линии относится к виду – жирафов, а ниже к виду – крокодилов:

x = input("Введите значение ширины Х: ")

x = int(x)

T = input("Введите значение высоты Y: ")

T = int(T)

y = A * x

# Условие

if T > y:

print('Это жираф!')

else:

print('Это крокодил!')

Функция input – принимает значение, вводимое пользователем. А условие гласит: если целевое значение (вводимое пользователем) больше ответа на выходе нейрона (выше красной линии), то сообщаем что – это жираф, иначе сообщаем что – это крокодил.

После ввода наших значений, получаем ответ:

Введите значение ширины Х: 4

Введите значение высоты Y: 15

Это жираф!

Теперь мы можем поздравить себя! Вся наша работа стала сводиться к тому, чтоб просто подавать на вход нейрона данные, не разбираясь в них самостоятельно. Нейрон сам классифицирует их и даст правильный ответ.

Если бы наши действия на работе сводились к подобным классификациям, то у нас появилась бы куча времени на кофе, очень важных общений в социальных сетях, и даже останется время, чтоб разложить пасьянс. И при всем этом можно выполнять ещё больший объём работы, что конечно же должно вознаграждаться премиальными и повышением зарплаты.

Теперь представим, что нам приходит новое задание. Где, проанализировав самостоятельно данные, мы видим, что их координаты значительно отличаются от прежних. Теперь провести классифицирующую прямую, обладая в своем арсенале лишь коэффициентом крутизны – не выйдет!

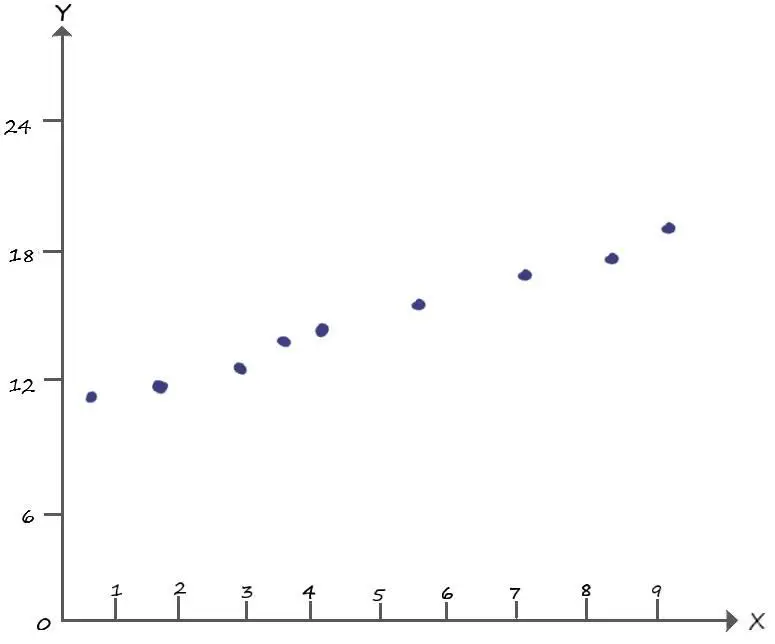
Очевидно, что без параметра b, которого мы до этого избегали ( b=0), тут не обойтись.