Геннадий Кривецков - Единая Теория Мироздания. Книга 2. Структуры, матрицы и силы Абсолюта

Сейчас возникает фантастическое предположение: а что, если эти две двойственные планетарные системы 1-го и 7-го уровней, образующие в сумме четыре системы, получаются у нас полностью тождественными и принадлежащими или Трансценденту, или 1-ому планетарному уровню, что может получиться одним и тем же?

Нам сложно своим разумом согласиться с таким предположением, ведь дело состоит в том, что Трансцендент имеет практически бесконечно большие параметры Пространства и Времени, а 1-ый планетарный уровень – их бесконечно малые параметры. И там, и здесь – бесконечность. Их фазы состояния отличаются на величину С т(90 0). Точно на такую же величину отличаются фазы 4-ого планетарного уровня. Здесь мы опять видим полное совпадение.

У нас всё сходится к тому, что 7-ой уровень Трансцендента и 1-ый планетарный уровень, если не обращать внимание на их пространственно-временные параметры, получаются полностью тождественными по своей структуре планетарными системами. Только этого мы никак не можем своим разумом принять: как большая бесконечность может быть равной меньшей бесконечности?

Это будет полным математическим нонсенсом. Но здесь просматривается ещё одна закономерность: протяжённость 4-ёх периодов их малых кругов всегда остаётся равной С ви для 1-ого планетарного уровня, и для Трансцендента. Тогда все соотношения в параметрах этих систем будут полностью тождественными, только величины Пространства и Времени в них будут разными.

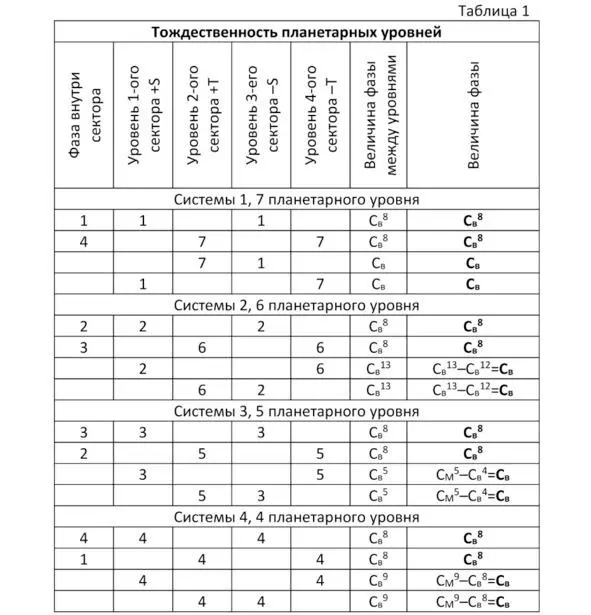
Все наши доводы осторожно доказывают тождество в соотношениях параметров структур 1-ого планетарного уровня и Трансцендента 7-го уровня. Мы пока согласимся с этим предположением, ведь других систем, которых нам недостаёт, мы более обнаружить не можем. Если это так, тогда все остальные планетарные уровни также должны иметь по четыре тождественных систем в своей структуре. Давайте это проверим, для чего составим таблицу 1 тождественности планетарных уровней.

В таблице 1 мы видим, что соотношения фаз между предполагаемыми нами тождественными системами 1—7, 2—6, 3—5, 4—4 получаются одинаковыми. Например, в двух системах 2 и 6 планетарных уровней мы видим по соотношению их параметров соответствие системам 4-ого уровня. Фаза разности между двумя этими уровнями будет равна С в 13, если вычесть из неё С в 12кратную 360 0, то мы получим ту же С в 13—С в 12=С в, что и в системах 4-ого уровня. Точно такая же ситуация с 3-им и 5-ым планетарными уровнями, которые также можно признать тождественными и объединить в одну четырёхмерную систему. Фаза разности между двумя этими уровнями будет равна С в 5, если вычесть из неё С в 4=360 0, то мы получим ту же величину С в 5—С в 4=С в, что и в системах 4-ого уровня.

По нашему предположению, практически уже доказанному, мы получаем в ПСМПр по 4-е полных четырёхмерных планетарных систем в четвёрке планетарных уровней (4×4), но обладающих разными пространственно-временными параметрами. Они все будут соответствовать единой ЭСН рисунка 10а только для своих планетарных уровней.

Вывод можно сделать довольно интересным: планетарные системы всех четырёх ЭСМ ПСМПр будут тождественными и даже, можно сказать, однотипными между собой по своей структуре и даже в соотношениях их параметров. Мы тогда получаем следующую последовательность соответствия по планетарным уровням: 1—7; 2—6; 3—5; 4—4. Только планетарные системы ЭСМ Времени будут располагаться зеркально планетарным системам ЭСМ Пространства. Они будут обращёнными относительно друг друга, что мы и видим в этой последовательности соответствия планетарных уровней.

Совершенно неожиданно у нас возникло понятие «Матрицы планетарных уровней». Глядя на таблицу 1, мы невольно обратили внимание на расстановку в ней значений планетарных уровней. Это натолкнуло нас на мысль о том, что эти номера планетарных уровней могут составить значения для матрицы ПСМПр. У нас получается по четыре планетарных уровней в четырёх ЭСМ, что нам даёт возможность составить матрицу с ячейками 4×4. Давайте попробуем изобразить её в таблице 2.

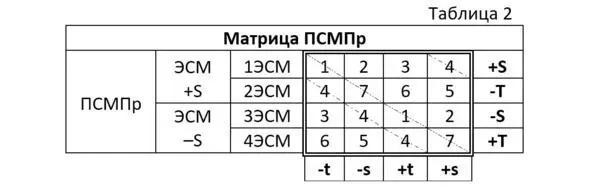
С первого раза покажется, что мы распределили планетарные уровни просто так, как нам этого захотелось, чтобы получить по диагоналям тождество по номерам уровней, которое мы получили в таблице 1. Мы показали его на диагоналях матрицы для двух планетарных уровней 4—4 и 1—7. Точно такое же диагональное тождество можно найти между 3—5 и 2—6 уровнями. Они получились у нас сами по себе. Мы специально под них матрицу не подгоняли. Давайте рассмотрим то, как мы распределяли планетарные уровни в этой матрице.