Сергей Бердышев - Открытия и изобретения, о которых должен знать современный человек

Подъемная сила исполина, разработанного в США (т. н. бостонский проект), достигает 380 т. Общая мощность двигателей в 6000 л.с. позволяет дирижаблю развивать скорость до 150 км/ч. Трехпалубное воздушное судно рассчитано на одновременную перевозку 400 пассажиров.

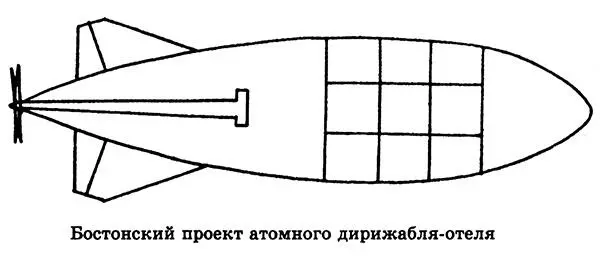
Это немного в сравнении с океанскими лайнерами, однако не нужно думать, будто люди будут тесниться на борту дирижабля. В проекте предполагается, что гостиница будет иметь все удобства. В ее плане имеется роскошный ресторан, танцевальный зал, видеосалон и т. д. Некоторые из постояльцев смогут взять с собой в путешествие личную машину: на борту предусмотрен гараж для перевозки 100 автомобилей.

Рано ставить точку и в военной истории дирижабля. Американцы предполагают использовать крупные дирижабли с мягкой оболочкой для патрулирования морских границ. Подобная техника поступила в управление береговой охраны США сравнительно недавно. Первым успешным дирижаблем стал самый большой на то время из имеющих мягкую оболочку «Сентинел-1000». Гигант обладает высокой маневренностью и может находиться в полете около суток без дозаправки. Исполин был построен и испытан в 1991 г.

Современная механика, основывающаяся на законах Ньютона и Галилея, сильно отличается от ранней классической механики. Во все времена эта наука служила потребностям производства. Сегодня ее значение в данной роли только возросло. Но поскольку запросы промышленности стали совершенно иными, то и механика претерпела серьезные изменения. Ее теоретическая часть дополнилась удивительными открытиями, а прикладная часть, как и следовало ожидать, обогатилась многочисленными изобретениями. Это связано главным образом с возникновением особой, «производственной» механики, которая распалась на автоматику, мехатронику, робототехнику и прочие направления.

Народная мудрость предостерегает нас: «Не говори „гоп“, пока не перепрыгнешь!». В этой нехитрой рекомендации заключен глубокий смысл, если подходить к ней с научных позиций. Выполнение любой работы требует от человека четкой последовательности действий. Сегодня в развитых странах повсеместно происходит активный процесс автоматизации труда, т. е. замены человека на тяжелых и вредных производствах машинами. Несложно догадаться, что данное незыблемое правило распространяется и на автоматы, а потому играет исключительно важную роль в развитии промышленности.

Описание последовательности действий мы называем указаниями или руководством. Наука использует название алгоритма. Прыгай, а потом говори «гоп» — типичный пример алгоритма, поскольку это руководство содержит описание оптимальной последовательности действий. Выполняя действия в указанной последовательности, можно добиться желаемого результата.

Само слово «алгоритм» имеет арабское происхождение. Это латинизированная форма от имени великого среднеазиатского математика прошлого аль-Хорезми. Он первым рассмотрел поиск решения задачи в качестве системы операций, осуществляемых в полном соответствии с правилами математического вычисления. Впоследствии составление приемов решения задач получило название алгоритмирования, а раздел математики, занимающийся данным направлением, был назван теорией алгоритмов.

Математика лежит в основе всех точных и технических наук, а также тесно сотрудничает с науками естественными. Невозможно назвать такую отрасль знания, которая не опиралась бы на математику. Оказывается, даже гармонию искусства можно «поверить алгеброй». Наверное, оттого столь величественны и прекрасны египетские пирамиды, что их творили любящие свое ремесло геометры. Для современного человека наиболее значимым достижением этой науки явилось начало изучения информации математическими методами.

Связь алгоритмов с трудовыми действиями, последовательностью чего-либо и с математическими величинами была установлена не сразу. Сначала математика взялась за проблему установления количественных законов доказательств и опровержений. Прежде чем изобрести научное алгоритмирование, требовалось заложить основы математической логики. Ее создателем выступил английский математик Дж. Буль, отчего долгое время, почти до 1950-х гг., данную дисциплину именовали «булевой алгеброй». Буль создал свою алгебру в 1854 г., указав на возможность применять математические законы для решения практических задач.