Arkady Serkov - Verification of M.Faraday's hypothesis on the gravitational power lines

In addition to continuity properties and properties when the "vacuum fluctuations, introducing virtual particles may exert pressure on the body," described in the literature [2], based on indirect evidence suggests that the physical vacuum is a viscous-elastic body whose properties can be characterized by the value of modulus and viscosity coefficient.

In materials science for objects with extremely high elastic properties are widely used methods for determining the modulus of elasticity of materials on the propagation velocity of ultrasonic waves. The higher the speed of propagation of ultrasound is the higher modulus material. The velocity of propagation of electromagnetic and gravitational radiation in the physical vacuum is very high, respectively, 2,998.10*10 and 2,3.10*8 cm / s. Consequently, we can assume that the physical vacuum as the medium in which the radiation propagates, has a high modulus of elasticity.

As for the viscous properties of the physical vacuum, they are similar to the rotational viscometer can be detected by slowing the speed of rotation of celestial bodies. Be reliably defined for the Earth and is about 0,001s for 100 years. This is secular slowing down the speed of rotation of the Earth. It is usually explained by the action of tidal forces of the Moon and the Sun. However, the inhibitory effect of the viscosity of the physical vacuum (physical environment) is also quite likely.

Another well-known fact testifies to delay the speed of rotation of celestial bodies in the process of evolution – a decrease in the rate of rotation of stars in the Main sequence. It is assumed that at the initial stage of evolution the equatorial rotation speed of the stars reaches 10 – 100 km / s. At the stage at which the Sun is located, it is 2 km / s, and continued to decrease until the release of the Main sequence.

Consider the possibility of quantifying the approximate viscous braking of the rotating cosmic body due to its shear interaction with the physical environment (physical vacuum).

Figure 1 show a diagram of this interaction, which can be used to calculate the "viscosity" of the physical vacuum. Rotating cosmic body (1) with a radius R slows its rotation under the effect of tangential force f, which is caused by the viscous resistance of the surrounding physical environment (physical vacuum). The linear velocity of the medium at the equator is the linear velocity of the body v. As the distance from the center of the body linear velocity of the medium due to its viscosity decreases to zero at the boundary of the action of the gravitational field of a rotating body at a distance Rg. To calculate the viscosity can use the Newton's law:

f = μ. (Δv / ΔR). s, (1)

where f – tangential force, causing the shear of the physical environment, μ – viscosity coefficient, Δv / ΔR – velocity gradient and s – area of the layer on which there is a shear.

Using the expressions (1) to and date on the slow the rotation speed of the Earth earlier [3] was calculated the viscosity of the physical vacuum and then after the resulting viscosity a value was estimated the deceleration of the Sun rotation speed.

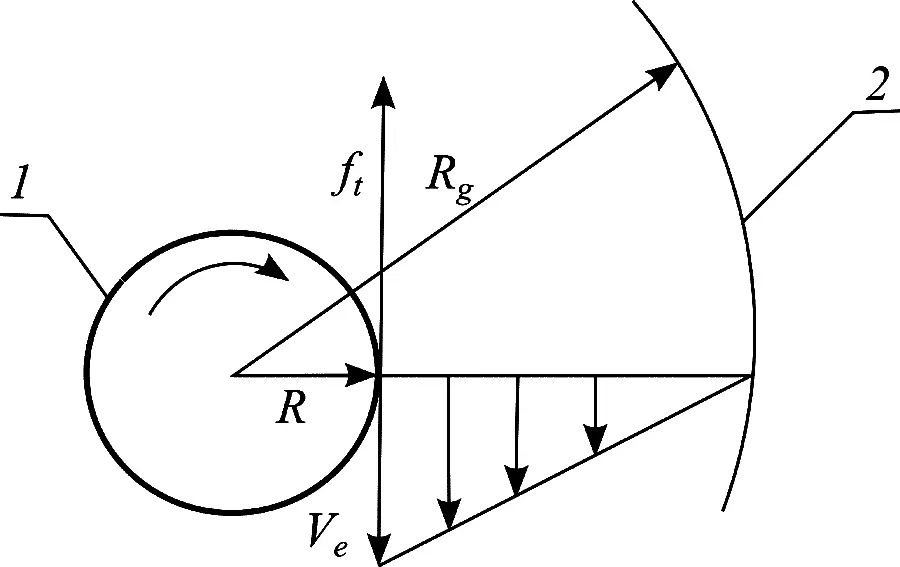
Fig. 1. Scheme of braking speed rotation of the cosmic body due to the viscosity of the physical vacuum: 1 – rotating body, 2 – border effect of the gravitational field of a rotating body, f – tangential braking force, v – equatorial velocity, R – radius of the body, Rg – radius of the sphere of action of the gravitational field formed body.

Also, based on indirect evidence can be seen on the property of the physical vacuum, undergo longitudinal and shear deformation. Moreover, due to the high modulus tensile longitudinal strain apparently is small. Shear deformation occurs during the formation of gravitational waves, which, by analogy with electromagnetic are apparently cross.

Cosmic body creates around itself a force field – the gravitational field. The main characteristic is its gravitational strength tension at any point. It characterizes the force which acts on a point located in this different body. The tension is given by:

g = F / m, (2)

where g – the field strength (tension), F – gravitational force, m – mass of the test body made to the field.

The gravitational field can be described analytically by calculating it's intensity for each point of the field or graphically, causing tension in the plot line or field lines. An example of a graphic image of the gravitational field is shown in Figure 2. Power lines or tension lines (1) begin at cosmic body (2) and extend into the surrounding space according to the formula (2) to infinity. When interacted many bodies the line tension can take a curved shape and then on the graph the field strength can be characterized by density of the location of power lines.

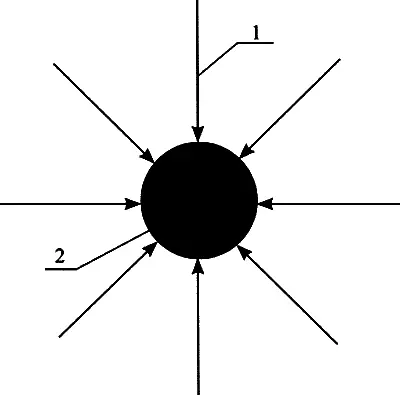
Fig.2. Schematic representation of the gravitational field: 1 – line tension (power line), 2 – cosmic body.

In accordance with the above concept to consider the surrounding physical environment induced in her gravitational field as elastic-viscous body can be assumed that this body has the ability to tensile strain and shear. The greatest interest is the shear deformation, which during rotation of the body can cause a concentric orientation of the force lines and thus reduce the resistance of the field orbital motion space bodies.

The interaction of a rotating body with elastic-viscous gravitational field, like other elastic-viscous fluids (liquids, gases) can be considered within the theory of dynamic boundary layers. However, with a persistent finding in the literature [4], it is almost not possible to find data on formation the boundary layers the rotating bodies.

The closest well-studied case can be considered a tear flow when the fluid flow separates from the surface of the curved shape. At the front of the body curved shape (Fig. 3) the flow velocity in the boundary layer decreases from the value v 0on the outer edge of the layer and to v = 0 on the body surface, At the point s there is separation of a laminar boundary layer, and turbulization of the flow.

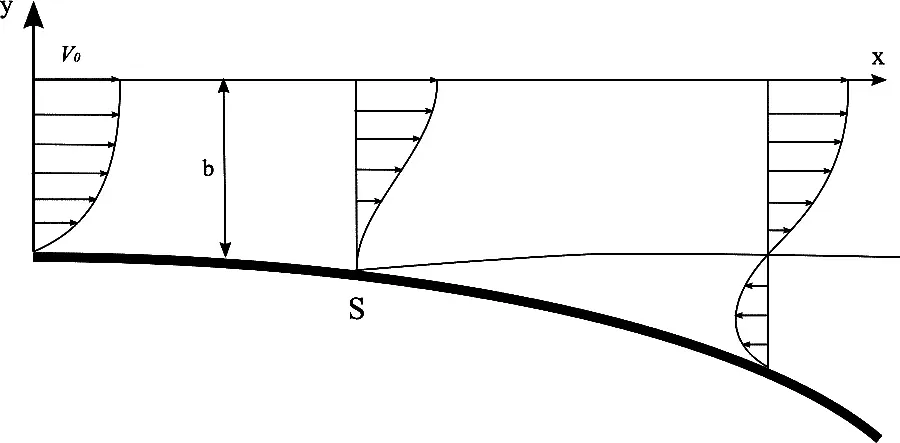
Fig. 3. The scheme of formation of separated flow around the flow body with a curved generatrix: v 0is the flow velocity, s – point margin, δ – thickness of the boundary layer.

Given that according to the accepted concept to consider the gravitational field as a viscous-elastic medium, we can assume that during the rotation of a celestial body around it will produce dynamic laminar layer δ, the thickness of which will depend on the mass and speed of its rotation and to meet space scale (tens to hundreds of thousands of miles).

Figure 4 provides a diagram of the dynamic boundary layer (2) of the gravitational field on the surface of a rotating spherical celestial body (1). The body rotates at a linear velocity v 0. Due to the viscosity of the environment (physical vacuum) formed in the boundary layer, the velocity gradient. On the body surface at point s, the velocity of the particles of the physical environment is equal to the linear velocity of the body v o. As the distance from the surface it drops to zero at the surface boundary layer.

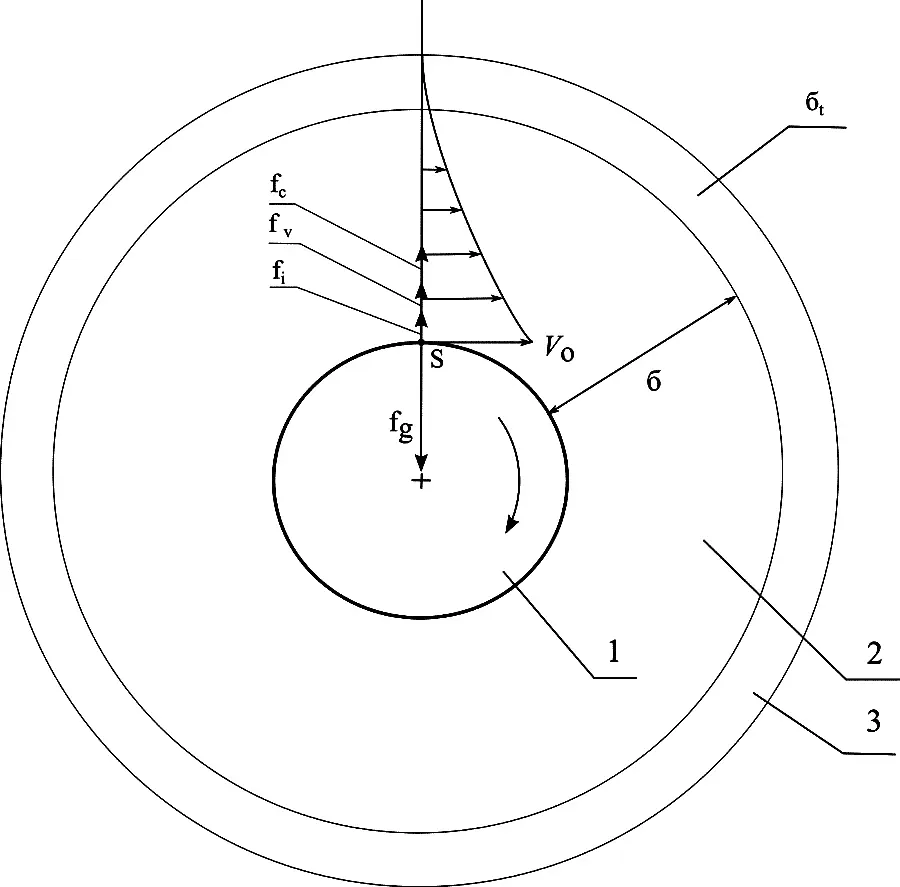
Fig.4. The formation of a boundary layer δ around the rotating sphere: 1 – rotating sphere, 2 – laminar boundary layer, 3 – turbulent boundary layer, v o– linear speed on the surface of a sphere, s – point separation, fg is the gravitational force, fc is the centrifugal force,