Микаэль Лонэ - Теорема зонтика, или Искусство правильно смотреть на мир через призму математики

Как и в случае с законом Бенфорда, эти ситуации ставят нас в логический тупик только потому, что мы думаем неверно. Потому что мы используем математический инструментарий, который плохо понимаем, в контексте, в котором он неуместен.

Как же тогда воплотить эти интуитивные размышления в математике? Ответ можно найти в тонком понятии порядка величины.

Сама идея простая, но невероятно мощная. Думать посредством порядка величины – значит думать с помощью умножения, а не сложения.

Если вы хотите сравнить числа 2 и 10, вы можете сделать это двумя разными способами. Путем сложения: сколько нужно добавить к 2, чтобы получить 10? В таком случае ответ 8. Или путем умножения: на сколько нужно умножить 2, чтобы получить 10? Тогда ответ равен 5. В первом случае разница между двумя числами получается путем вычитания: 10 ÷ 2 = 8. Во втором – деления: 10 ч 2 = 5.

Сказать, что два числа имеют одинаковый порядок величины, значит сказать, что они близки с точки зрения умножения.

Несмотря на то, что на первый взгляд эта идея кажется довольно странной, любой, кто начинает мыслить мультипликативно, то есть посредством умножения, быстро понимает, насколько этот подход лучше соответствует нашей интуиции.

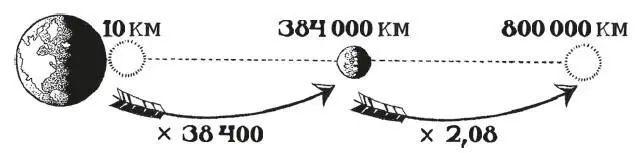
Вернемся к нашей научной викторине. Вот как я мог бы отстоять нашу победу в игре, если бы тогда мыслил здраво. Луна находится на расстоянии 384 000 километров от Земли, а наша команда ответила, что на расстоянии 800 000 км, то есть примерно в два раза дальше. Если мы поделим числа, то окажется, что наш ответ был в 2,08 раза больше верного. Наши противники ответили, что расстояние составляет 10 км, то есть в 38 400 раз меньше правильного ответа! С этой точки зрения мы действительно победили. Более того, этот результат гораздо лучше соответствует нашему интуитивному восприятию мира.

Такой подход сработает и со всеми остальными примерами. Если считать мультипликативно, то размер кошки ближе к размеру собаки, чем к размеру бактерии, масса Марса ближе к массе Земли, чем к массе мячика для пинг-понга, население Парижа ближе к населению Нью-Йорка, чем к населению маленькой деревни, и так далее.

Когда мы сравниваем два числа, независимо от контекста, в котором происходит это сравнение, чаще всего мы интуитивно прибегаем к мультипликативному мышлению. Если в вашем супермаркете товар стоимостью 200 евро подорожает на 8 евро, то, несомненно, это подорожание вас расстроит, но гораздо меньше, чем если бы на те же 8 евро подорожал товар стоимостью 2 евро. В таком случае цена увеличивается до 10 евро, то есть в 5 раз! Расстроиться – это мягко сказано. И это при том, что номинально цены выросли на одну и ту же величину.

Таким подходом к сравнению мы обязаны не только работе интеллекта. Это не уникальное свойство мышления, он естественен для нас и моделирует большинство наших взаимодействий с миром. Наше чувственное восприятие окружающего мира тоже мультипликативно.

Если я завяжу вам глаза и вложу в одну руку предмет весом 10 г, а в другую – весом 20 г, вы сразу же поймете, какой из них тяжелее. Но различить «на ощупь» предметы весом 10 кг и 10 кг и 10 г куда сложнее. Однако разница в парах одинаковая: 10 г. Или, точнее, разница одинаковая с точки зрения сложения, или аддитивности, потому что с точки зрения умножения она вопиющая: 20 г в два раза тяжелее, чем 10 г. Во втором же случае разница между двумя массами составляет всего 0,1 %.

То же можно сказать и про наше зрение. Вы когда-нибудь пробовали включить свет средь бела дня? Если солнце уже заливает комнату, это почти ничего не меняет. Яркость кажется одинаковой независимо от того, светит лампочка или нет. Но если вы включите свет ночью, то ясно увидите, как он освещает самые темные уголки, которые мгновение назад терялись в полумраке.

Тем не менее днем лампочка излучает не меньше света, чем ночью. То есть с точки зрения сложения яркость одинакова в обеих ситуациях. Но наши глаза воспринимают эту яркость иначе – относительно, то есть мультипликативно. При дневном свете яркость лампочки незначительна по сравнению с яркостью Солнца. Ночью же все меняется – она правит бал.

Это справедливо и для остальных органов чувств: осязания, зрения, вкуса, слуха, обоняния. Подумайте хотя бы о том, как вы воспринимаете течение времени, преодоленное расстояние, и, что более субъективно, интенсивность эмоций, которые испытываете. Все эти чувства гораздо проще поддаются пониманию, когда вы начинаете думать о них мультипликативно, а не аддитивно.