М. Нсанов - Цифровые устройства. Учебник для колледжей

Рассмотрим примеры объединения клеток.

1. В карте Вейча с 8 клетками (рис.2.7).

2. В карте Вейча с 16 клетками (рис.2.8).

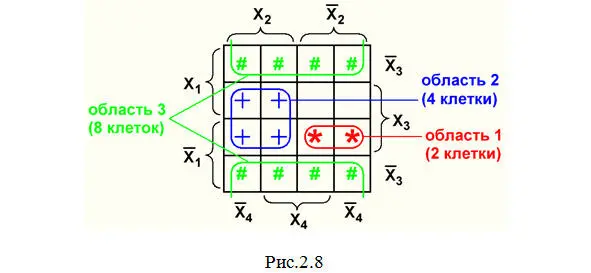
В каждой такой области объединения выполняется операция «склеивания», в результате которой остается только один многочлен только с теми переменными, которые входят во все объединенные клетки. А переменные типа X 1и X 1′, X 2и X 2′, X 3и X 3′, X 4и X 4′«сокращаются». Это можно объяснить на следующем примере: возьмем два многочлена СДНФ (аналогичный результат получается и с многочленами СКНФ), соответствующих двум клеткам области 1 рис.2.7:

Х 1·Х 2·X 3′ \/ X 1·X 2′·X 3′;

одинаковые переменные вынесем за скобки:

X 1·X 3· (X 2\/ X 2′);

легко проверить, что выражение в скобках при любых значениях X 2( 0 или 1) дает 1, тогда:

X 1·X 3·1 = X 1·X 3.

Итак, в результате «склеивания» двух клеток области 1 рис.2.7 получается: X 1·X 3.

Приведем примеры (рис.2.10) «склеивания» клеток в карте Вейча на рис.2.4:

Очевидно, что при объединении всех клеток любой карты сокращаются все переменные, и результат «склеивания» дает 1.

Из сравнения полученных результатов можно сделать вывод : чем больше объединяется клеток, тем проще получается результат «склеивания» , т.е. итоговое логическое выражение содержит меньше операций, и, соответственно, схема ЦУ будет иметь меньше логических элементов.

Теперь приведем порядок минимизации :

– Чертим карту Вейча с нужным количеством клеток.

– Клетки карты, соответствующие минтермам СДНФ (или СКНФ) обозначаем символом « 1».

– Объединяем все клетки с « 1». Количество клеток в каждом объединении должно быть максимальным, а самих областей объединения должно быть как можно меньше. П р и м е ч а н и е: любое количество клеток с « 1» могут одновременно входить в две или больше области объединения.

– В каждой области производим операцию «склеивания», в результате чего получаем многочлены минимальной формы: МДНФ или МКНФ.

Приведем несколько примеров минимизации:

Пример 1. Минимизация СДНФ функции Y 1из темы 2.1 (рис.2.11):

Покажем на рис.2.12 результаты"склеивания» двух клеток в областях 1 и 2 этой карты.

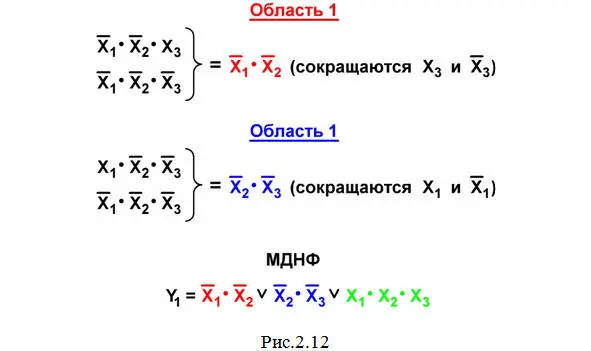
Область 3 : Эта клетка остается одна – ни с какими другими клетками, содержащими « 1», ее объединить нельзя. Поэтому соответствующий данной клетке многочлен Х 1·Х 2·Х 3не сокращается и входит в минимальную дизъюнктивную нормальную форму (МДНФ) без изменения.

В результате на этом же рис.2.12 записываем МДНФ ( красным, синими зеленымцветом показаны минтермы, которые получились в результате «склеивания» клеток в областях объединения соответствующего цвета на рис.2.11).

Пример 2 . Минимизация СДНФ функции Y 2из темы 2.1 (рис.2.13):

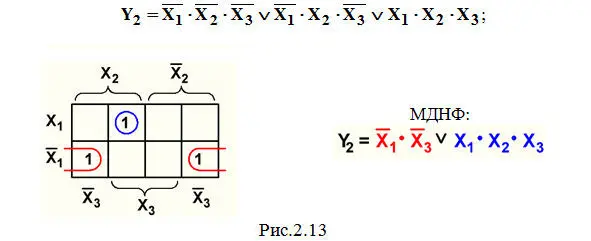
Пример 3 . Минимизация СДНФ функции Y 3из темы 2.1 (рис.2.14):

Совершенно аналогично выполняется минимизация логических функций, записанных в СКНФ. Рассмотрим примеры:

Пример 4. Минимизация СКНФ функции Y 1из темы 2.1 (рис.2.15):