Аркадий Серков - Общая теория поля и структура вселенной

Теперь продемонстрируем действие рассмотренных законов в широком диапазоне атомных параметров. Начнём с крайних случаёв с самой коротковолновой серии рентгеновского излучения и строения атома урана, обладающего наибольшей атомной массой.

Рентгеновское излучение α 1в серии K атома урана имеет самую короткую длину волны 0,01259 нм. Поэтому можно полагать, что такая длина волны (частота) соответствует минимальному квантовому числу n= 1 и радиусу орбиты, то есть в соответствии с уравнением (4) для первой орбиты k = r. В свою очередь, зная длину волны λ, рассчитываем радиус по уравнениям 3-го закона Кеплера , которые применительно к атомным системам имеют вид:

λ= 2π c r 1,5 /( gmd ) 0,5, (9)

ν = ( gmd ) 0,5/2π r 1,5, (10)

где λ- длина волны, ν- частота излучения, с – скорость света, r – радиус орбиты, g – константа микро гравитации, m – атомная масса, d – дальтон.

Подставив в уравнение (9) приведенные выше значения величин, получим радиус первой орбиты атома урана, с которой происходит рентгеновское излучение серии K α 1 , r= 0,069 пм. Радиусы других орбит рассчитываем по уравнению Бора (4) умножением на квадрат соответствующего орбите квантового числа, см. таблицу 1. Так, например, для следующей рентгеновской L серии при n = 2 получена длина волны λ cal= 0,1011 нм при справочном значении λ exp = 0,07479 ни, а для М серии при n= 3 соответственно λ cal = 0,3412 нм и λ exp = 0,3329 нм. Для других серий при n= 4, 5, 6 и 7 также получено хорошее совпадение расчётных и экспериментальных данных, см. столбцы 6 и 7 в таблице 1.

Таблица1. Параметры атома урана.

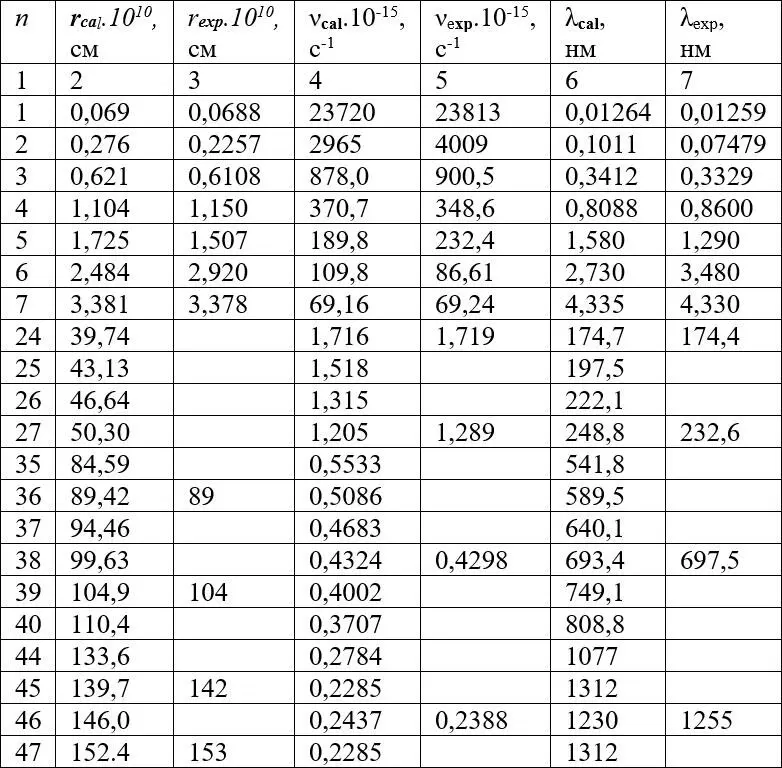
Удовлетворительное совпадение также наблюдается для расчетных и экспериментальных значений атомных радиусов, характеризующих длину химических связей и размер атома, см. столбцы 2 и 3. Рассчитанные по уравнениям (1) и (2) длины связей равны 89,42 и 104,9 пм. Экспериментальные значения почти совпадают с этими величинами и равны соответственно 89 и 104 пм. Расчётная длина ковалентной связи равна 139,7 пм, экспериментальное значение 142 пм. Наконец, расчётный радиус атома урана 152,4 пм практически совпадает с экспериментальной величиной 153 пм.

Достоверность модели строения атома урана подтверждается совпадением частот излучения, рассчитанных по уравнению Бальмера-Ридберга и частот рассчитанных по уравнению 3-го закона Кеплера, в котором использовали радиус r , рассчитанный по уравнению Бора (4).

Уравнение Бальмера-Ридберга выражает изменение частот излучения в зависимости от двух рядов квантовых чисел n i и n j :

ν = cR (1/ n i 2 - 1/ n j 2 ), (11)

Здесь с – скорость света, R 0 – постоянная Ридберга, которая длительное время была известна только для водорода. В нескольких работах [12] было показано, что постоянной Ридберга для химического элемента является его энергия первой ионизации. Для урана она равна 7,11 эВ или 11,39.10 -12эрг или в обратных сантиметрах ν 0= ν/с = 0,5734.10 5см -1. Таким образом, имеется возможность рассчитать частоты по уравнению Бальмера-Ридберга для урана и сравнить их с частотами, рассчитанными по уравнениям Бора (4) и 3-го закона Кеплера (9). Результаты таких расчётов представлены в таблице 1 столбцы 4, 5, 6 и 7.

Частоты и длины волн в столбцах 4 и 5 для квантовых чисел 24–47 рассчитывали по уравнениям 3-го закона Кеплера (9) и (10) с использованием величины радиуса, рассчитанного по уравнению Бора (1). По уравнению Бальмера-Ридберга рассчитывали характерные частоты и длины волн, которые можно сравнить с рассчитанными по 3-ему закону Кеплера. К числу последних относятся предельные и головные частоты.

Предельные частоты реализуются, когда второе квантовое число n j = ∞ и рассчитываются по уравнению:

ν = cR/n i 2 , (6)

где R 0 – постоянная Ридберга , равная для урана 0,5734.10 5см -1.