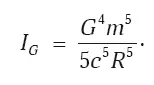Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Проиллюстрируем на простых примерах, какие системы излучают гравитационные волны, а какие – нет.

Рассмотрим сначала однородный шар, который пульсирует без изменения сферичности. Излучает ли гравитационные волны такой объект? Ответ – нет. Действительно, если сферичность не нарушена, то из наших рассуждений о потенциале следует, что на любой стадии пульсации квадрупольный момент просто не возникает. Приведем другой пример. Пусть любое аксиально симметричное однородное тело типа дыни вращается, а ось вращения совпадает с осью симметрии. Хотя «дыня» и имеет квадрупольный момент, но при таком вращении он не будет меняться. Значит, снова не будет излучения.

Теперь приведем простые примеры излучающих систем. Рассмотрим два тела одинаковой массы m и незначительных габаритов, соединенные пружинкой длины l. Выберем направление одной из осей координат, скажем 0 х , вдоль пружины, а середину пружины – за начало координат. У такой системы будет единственная независимая ненулевая компонента D . В состоянии покоя это D xx = ml 2. Через нее определяются D yy = D zz = — D xx /2. Теперь заставим грузы колебаться относительно своих положений равновесия с амплитудой L и частотой. Тогда компоненты квадрупольного момента станут переменными :

D хх ( t ) = ml 2+ 4 mL ( l cos ω t + L cos 2ω t ).

Соотношение D yy = D zz = — D xx /2 сохранится. Производная по времени третьего порядка этих величин ненулевая, значит, система излучает гравитационные волны.

Другой пример ближе к жизни, и мы рассмотрим его подробнее. Пусть две звезды одинаковой массы m , вращаются по одной и той же окружности вокруг общего центра масс. Они все время находятся друг против друга на расстоянии 2 R (рис. 10.3). Пусть плоскость орбиты совпадает с плоскостью x 0 y , а угловая частота вращений равна ω, она связана с орбитальным периодом как T = 2π/ω. Тогда ненулевыми компонентами квадрупольного момента являются:

D xx = 2 mR 2 (3 cos 2ω t – 1), D yy = 2 mR 2(3 sin 2ω t – 1),

D xy = 3 mR 2sin2ω t, D zz = – 2 mR 2

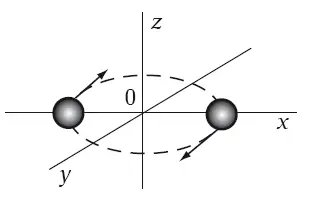
Рис. 10.3. Модель двух звезд

Начальное состояние соответствует t = 0, массы расположены на оси 0 x . В данный момент компоненты квадруполя будут такими же, как в модели с пружинкой, т. е. независимой является только одна компонента.

Конечно, и такая система должна излучать. Поскольку движение обусловлено гравитационным взаимодействием, то и R связаны уравнением m 2 R = Gm 2/4 R 2. Тогда, после усредненияя по периоду и представления через R , мощность гравитационного излучения выражается формулой:

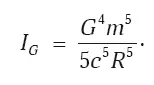
Система излучает тем интенсивнее, чем меньше R (или чем больше частота вращения, как следует из их уравнения связи).

Чтобы проиллюстрировать насколько мало гравитационное излучение, приведем следующий пример. В Солнечной системе, наибольшая мощность гравитационного излучения возникает в паре Солнце + Юпитер. Это излучение можно рассчитать по аналогичной формуле. В результате получим примерно 5 кВт (это всего лишь мощность пяти больших бытовых кипятильников советских времен). Энергия, теряемая Солнечной системой на гравитационное излучение за год, совершенно ничтожна по сравнению с кинетической энергией этих тел.

Необходимо сказать несколько слов о направленности гравитационного излучения. В случае с грузами на пружинке по ее оси вообще нет излучения, а максимум – в направлении перпендикулярном пружинке. В случае кругового движения интенсивность излучения в направлении перпендикулярном плоскости орбиты в несколько раз больше, чем в направлениях, лежащих в плоскости. Связаны эти особенности с тем, что излучаемая гравитационная волна является поперечной.

Слабость гравитационного излучения оставляет мало шансов для его регистрации. Где же искать подходящие источники? Наш соотечественник, замечательный физик-теоретик Владимир Фок (1898–1974), рис. 10.4, был первым, кто в 1948 году обратил внимание на возможность детектирования гравитационного излучения, возникающего при астрофизических катастрофах. Детальный анализ позволяет сделать вывод, что наиболее перспективными источниками гравитационных волн будут компактные объекты, размеры которых сравнимы с гравитационным радиусом, а скорости сравнимы со скоростью света. Согласно расчетам, при слиянии двух нейтронных звезд излучается около 10 45Дж в виде всплеска гравитационного излучения, т. е. около 1 % от их полной энергии.