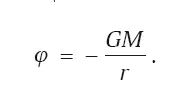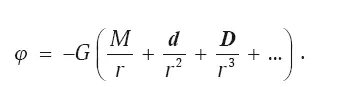Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Относительное изменение расстояния между двумя пробными частицами в поле плоской гравитационной волны определяется выражением ∆ l/l ≈ h /2. Это соотношение показывает, что по своему физическому смыслу амплитуда является безразмерной величиной. Часто ее называют «безразмерной амплитудой возмущений метрики», создаваемых гравитационной волной. Кроме того, важен угол между направлением распространения волны и отрезком, соединяющим частицы. В силу поперечного характера, если эти направления совпадают (угол нулевой), то эффекта не будет, если они ортогональны, то эффект максимален.

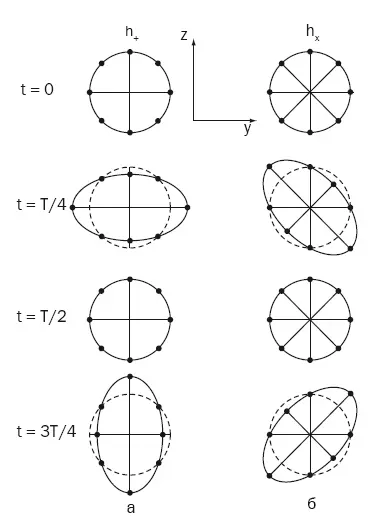
Рис. 10.2. Действие гравитационной волны

Гравитационное излучение чрезвычайно слабое. Это связано со слабостью гравитационного взаимодействия в природе. Например, электромагнитная константа связи (ее называют постоянной тонкой структуры) α= e 2/h c ≈ 1/137, где используются заряд электрона, постоянная Планка и скорость света. В то же время аналогичная безразмерная константа связи гравитационного взаимодействия имеет порядок α G = Gm p 2/h c = ( m p/ m Pl) 2 ≈ 10 –38, где используются масса протона и планковская масса. В отличие от электромагнитного излучения, когда каждый атом может излучить фотон, и его можно зарегистрировать, гравитационное излучение формируется большим количеством атомов, электронов и т. д. и становится существенным при несимметричном движении больших масс вещества (отдельных объектов) в целом.

Продолжая сравнение с электродинамикой, вспомним, что электромагнитное излучение генерируется переменным дипольным моментом. А при каких условиях возникает гравитационное излучение? Чтобы ответить на этот вопрос, объясним, что такое дипольный момент и моменты других порядков массивного тела.

Вспомним, что потенциал точечной массы в теории Ньютона

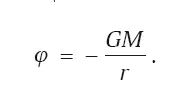
Если вместо точки взять сферическое тело (однородный шар) той же массы M с центром, где раньше была точка, то значение потенциала вне тела не изменится.

При несферичности рассматриваемого тела выражение для потенциала изменится, и изменения будут связаны непосредственно с отклонениями от сферичности. Величину отклонения можно представить так. Если сферическую составляющую принять за исходную симметрию, то первая степень отклонения (грубая) – дипольная, следующая (более «тонкая») – квадрупольная, и т. д. Тогда значение потенциала в выбранной точке можно представить в виде:

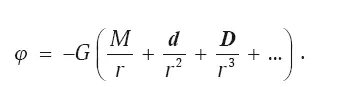
Здесь d – дипольный момент, а D – квадрупольный. Формула является символической: в ней не учтены коэффициенты, а также векторный и тензорный характер некоторых величин. Но она показывает, что при удалении от источника каждый из последующих членов ряда дает все меньший вклад в формирование потенциала.

В электродинамике излучение определяется изменением дипольнного момента (рис. 10.1) В гравитации дипольный момент, который является вектором, определяется следующим образом: из начала координат к каждому элементу массы Δ M проводится радиус-вектор R, после чего величины Δ M· R векторно суммируются по всем элементам массы. Ясно, что выбрав начало координат в центре масс, мы получим дипольный момент тождественно равный нулю. Это можно сделать всегда, поскольку в гравитации, в отличие от электромагнетизма, нет противоположных зарядов (нет отрицательных масс). Следовательно, не может быть и гравитационного излучения, связанного с дипольным моментом.

Гравитационное излучение возникает при изменении квадрупольного момента – D . Вспомним о моменте инерции , который является мерой инертности тела во вращательном движении, точно так же, как инертная масса – мерой инерции в поступательном движении. Квадрупольный момент – это момент инерции из которого исключена шаровая составляющая, определяющая основной (симметричный) вклад в потенциал.

Если в электродинамике мощность электромагнитного излучения пропорциональна квадрату второй производной по времени от дипольного момента, то в ОТО гравитационное излучение возникает из-за переменной асимметрии , определяемой квадрупольным моментом D , и мощность излучения пропорциональна квадрату третьей производной по времени от D. Значит, как бы тело не было деформировано, оно не излучает, если покоится.