Сергей Парновский - Как работает Вселенная - Введение в современную космологию

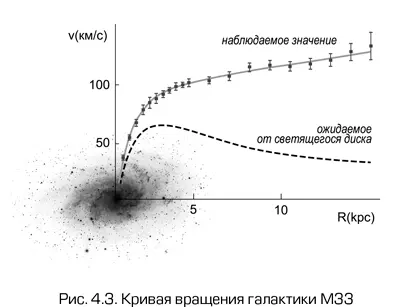
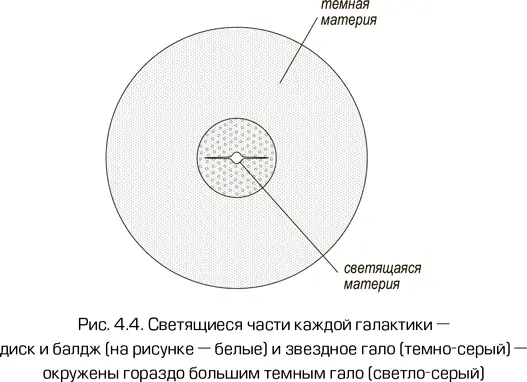
На рис. 4.3 показано изображение галактики M33 (Треугольник), входящей в Местную группу, т. е. одной из самых близких к нам галактик. На него наложена кривая вращения этой галактики таким образом, что масштаб расстояний совпадает с масштабом изображения. Обратим внимание, что кривая вращения приведена для области, существенно превосходящей видимые размеры галактики. Как это было сделано? Для этого использовались наблюдения небольших водородных облаков, вращающихся вокруг галактики вне ее видимой области. Естественно, закон Кеплера для них выполняется точно так же, как и для звезд. На рисунке кроме реальной кривой вращения изображена теоретическая кривая вращения, которую имела бы эта галактика, если бы вся ее масса была сосредоточена в светящейся компоненте. Легко понять, что за пределами видимой части галактики M(r) доля светящейся материи становится постоянной и v(r) в отсутствие темной материи падала бы по закону v ~ r–1/2. В то же время реальная кривая вращения, напротив, продолжает возрастать далеко за пределами видимой области, показывая, что там должно существовать нечто, вносящее вклад в общую массу галактики. Это и есть темная материя. Согласно существующим представлениям, все галактики окружены гало из темной материи (см. рис. 4.4), размеры которого существенно превосходят размеры видимой части галактики.

Если мы посмотрим на кривые вращения чуть более далеких галактик, то увидим, что v(r) иногда выходит на постоянное значение в широких интервалах изменения r. Такие кривые вращения называются плоскими. Забавно, что в Facebook даже была создана специальная группа сторонников того, что все кривые вращения можно считать плоскими. Эта группа с незатейливым названием «Кривые вращения галактик – плоские» выпустила по этому поводу свой меморандум. Вскоре после этого в той же соцсети появилась группа противников подобного обобщения, справедливо указывающая, что далеко не все кривые вращения галактик можно считать плоскими. Она также выпустила свой меморандум, а ее лидеры организовали серию научных семинаров по всему миру с целью развеять этот миф. К счастью, в научном мире справедливость той или иной гипотезы не определяется количеством лайков в социальных сетях.

Существует одна галактика, кривую вращения которой нельзя определить описанным выше способом. Это – наша Галактика, которую мы видим изнутри. Тем не менее кривая вращения нашей Галактики также получена астрономами, правда с меньшей точностью, чем для близлежащих галактик. Из параметров орбиты Солнца вокруг центра Галактики (радиус – 26 400 св. лет, период – 230 млн лет) по закону Кеплера нетрудно рассчитать массу материи, заключенную внутри орбиты Солнца, – она равняется 1,0×1011 M☉. Полная же масса нашей Галактики составляет около 1012 M☉.

Другой способ определения содержания темной материи связан с использованием отношения массы M светящегося объекта к его светимости L, которая обозначается Υ (греческая буква ипсилон). Поскольку массы звезд и галактик в астрономии традиционно меряются в солнечных массах, а светимости – в светимостях Солнца, эта величина измеряется в единицах отношения солнечной массы к солнечной светимости, равной Υ☉ = 5133 кг/Вт [71] Так что надо более 5 т солнечного вещества, чтобы произвести 1 Вт мощности. Если бы наиболее распространенная 60-ваттная лампа накаливания работала с той же эффективностью, ее вес был бы порядка 300 т — столько, сколько весят шесть танков, два тепловоза или нагруженный самолет C-5 Galaxy. . В давние времена астрономы при оценке масс исходили из того, что Солнце – типичная звезда. Они были почти правы, поскольку наиболее типичная звезда нашей Галактики – карлик с массой, вдвое меньшей массы Солнца. Поэтому, если светимость какого-то объекта, состоящего из звезд, в N раз превышала светимость Солнца, считалось, что его масса в N раз больше солнечной. Присутствие темной материи повышает массу, но не дает вклад в светимость. Поэтому исследования отношения массы к светимости для разных объектов позволяют говорить о наличии темной материи. Вблизи Солнца, где 99 % звезд слегка легче Солнца, Υ = (2,5–7) Υ☉, для звезд в галактическом диске Υ = (1–1,7) Υ☉, типичное значение для галактик Υ = (2–10) Υ☉.