Олег Власов - Футболоматика - как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния

«Барселона», возможно, построила лучшие треугольники в футболе, но треугольники решали проблемы и задолго до того, как появился футбол.

«Барселона», возможно, построила лучшие треугольники в футболе, но треугольники решали проблемы и задолго до того, как появился футбол. Рассмотрим следующую проблему. Вы – мэр города, в который входят несколько пригородов. Вы хотите построить железную дорогу, которая соединит их. Но вам не хватает денег, поэтому вы хотите использовать наименьшее количество рельсовых путей. Как вы соедините все пригороды с минимальной длиной железнодорожных путей?

Рисунок 2.2 показывает три правдоподобных решения для четырех пригородов. Посмотрите на них и подумайте, какой из них использует наименьшее количество ресурсов.

Если мы применим знания тригонометрии из средней школы, мы сможем выяснить, какой вариант наиболее короткий.

Решение слева состоит из трех блоков: каждая сторона по длине равна блоку и для соединения нам необходимы три стороны.

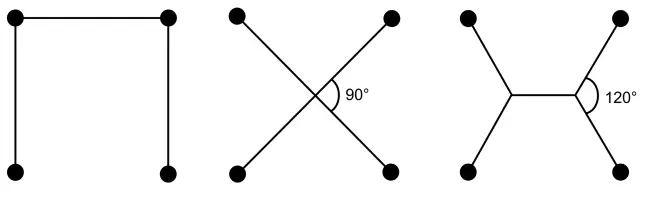
Рисунок 2.2. Три возможных решения для соединения четырех пригородов (круги) с наименьшей возможной длиной железной дороги (сплошные линии).

Решение посередине добавляет соединение в центр, разделяя область на четыре одинаковых треугольника. Длина каждой из двух пересекающихся линий может быть рассчитана с использованием теоремы Пифагора и равна √2. Общая длина равна √2 + √2 = 2,82 блока. Это решение похоже на расположение Хидегкути между полузащитой и форвардами или на то, как «Барселона» использует Месси. Добавление дополнительных точек дает треугольники, которые уменьшают общую длину соединительных линий.

Если одна дополнительная точка соединения – это хорошо, то использование двух еще лучше. На рисунке 2.2 длина правой структуры составляет 1 + √3 = 2,73 блока [13] Длина каждой из четырех ветвей, соединенных с пригородами, равна Применяя теорему Пифагора, средняя длина тогда . Общая сумма равна . – это наименьшее из всех решений. И снова задействованы треугольники. Три ответвления выходят из точек соединения под углом 120°. Как это часто бывает в математике, самая красивая и наиболее сбалансированная форма является лучшим решением.

Решение проблемы эффективного соединения четырех точек на квадрате было непростым (не могу сказать точно, сколько мэров справилось с этим). Но это задача для начинающих. Если хотите бросить себе настоящий вызов, попробуйте найти решение для пяти точек на углах пятиугольника. Ответом снова будут треугольники. Вопрос лишь в том, как их упорядочить. Если справитесь с пятью, попробуйте шесть точек в шестиугольнике. В последнем случае результатом станет совершенно новый тип решения, но он все еще включает в себя треугольники. Смотрите рисунок ниже.

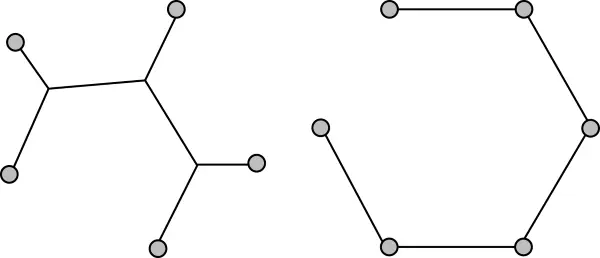
Ответ. Решение для пяти и шести точек.

Давайте сделаем проблему соединения пригородов действительно сложной. Попробуем решить эту проблему, если мы не знаем расположения пригородов или даже сколько их необходимо подключить. С такой проблемой постоянно сталкивается слизевик под названием Physarum polycephalum. Слизевики не имеют мозга и состоят всего из одной клетки. Их «тело» представляет собой сеть взаимосвязанных трубок, которые качают питательные вещества назад и вперед. Слизевиков можно обнаружить на лесной подстилке или деревьях. Обычно они покрывают площадь меньше монеты, однако они могут сжиматься в неблагоприятных условиях и разрастаться, если еды вдоволь.

Когда слизевики ищут еду, они решают проблему соединения пригородов. Вдохновленный этой идеей, мой японский коллега Тоси Накагаки решил проверить, смогут ли слизевики создать сеть метрополитена и скоростного трамвая Токио. Он и его коллеги разложили питание слизевиков в виде масштабной модели Большого Токио. Они положили овсяные хлопья в чашки Петри: одна большая посередине как отображение центра города и поменьше в местах, соответствующих Сибуе, Иокогаме, аэропорту в Тибе и другим близлежащим районам. Чтобы добиться соединения чашек с овсом, слизевики должны решить ту же проблему, которую разрешили японские градостроители при проектировании транспортной системы Токио. Могут ли слизевики формировать эффективные связи между своими продовольственными ресурсами?