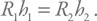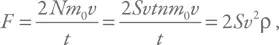
где m 0– масса молекулы.
Эта сила уравновешена силой тяжести, равной mg , где m – масса падающего тела, а g – ускорение свободного падения. Равенство двух сил позволяет вывести простую формулу для соответствующей скорости:
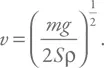
Зависимости прозрачны. Чем массивнее тело, тем быстрее оно будет падать. Чем больше плотность среды, тем меньше скорость. Большая площадь также позволяет уменьшить скорость падения (забыли парашют – распахните пальто).
Можно подставить какие-нибудь характерные значения и дать оценку скорости. Округляя, мы получим, что тело массой около 100 кг и площадью 1 кв. м может набрать скорость порядка 100 км/ч. Такая скорость набирается при падении с высоты метров 40. У человека площадь меньше, поэтому, с одной стороны, можно разогнаться до пары сотен км/ч [136] Желающие могут заглянуть в Википедию ( https://en.wikipedia.org/wiki/Free_fall ), где приводится значение предельной скорости – около 200 км/ч.
, а с другой – получить оценку, что парашют с площадью порядка 100 кв. м должен замедлять спуск до безопасных скоростей.
Приложение 9
Высота гор и форма астероидов
Уже более 300 лет назад астрономы могли убедиться, что наблюдаемые небесные тела (планеты и их спутники) имеют округлую форму. Однако очевидно, что камень (в том числе и летающий в космосе) может иметь довольно причудливую форму. Легко сообразить, в чем дело: гравитация придает крупным телам сферическую форму, «сглаживая» неровности, как мы, создавая давление руками, лепим круглые снежки.
Можно ли примерно оценить размер тела, при котором оно уже не сможет поддерживать заметно несферическую форму? Оказывается, сделать это легко. Надо всего лишь знать закон всемирного тяготения.
Догадаться о структуре закона, определяющего гравитацию, тоже можно. Во-первых, сообразить, что чем массивнее тела, тем больше гравитационное взаимодействие между ними. Во-вторых, из-за трехмерности однородного и изотропного пространства сила будет спадать как квадрат расстояния. Получаем известный из школьной физики закон:
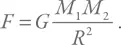
Здесь в числителе стоят массы притягивающихся тел. Нас будет интересовать ситуация, когда M 1– масса планеты, M 2– масса заметной неоднородности на ней (по сути, речь идет о горе на поверхности). А стоящая в знаменателе величина R – радиус планеты.
Теперь нам надо правильно сформулировать задачу на качественном уровне. Мы знаем, что самые высокие горы на Земле имеют высоту несколько километров. Давайте положим предельную высоту равной 10 км. Если гора будет более высокой, то породы в ее основании не выдержат давления, и гора осядет. Давление (обозначим его P ) равняется частному от деления силы на площадь (обозначим ее S ): P = F / S . Сделаем разумное предположение, что критическое давление будет одним и тем же для всех космических тел, интересующих нас. Запишем равенство критического давления в двух ситуациях:
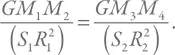
Слева – давление в основании горы массой M 2на первой планете с массой M 1и размером R 1, а справа – давление в основании горы массой M 4на второй планете с массой M 3и радиусом R 2.
Теперь, чтобы рассчитать силу, нам надо знать массу горы. Представим себе гору как конус. Его масса пропорциональна объему. Математика дает нам возможность рассчитать объем конуса. Он пропорционален произведению высоты ( h ) на площадь основания: 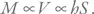 Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.
Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.
Масса планеты пропорциональна ее объему. Объем шара пропорционален кубу радиуса: 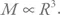 Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение:
Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение:
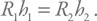
Нас интересует случай, когда второе тело имеет заметно несферическую форму, т. е. высота горы на второй планете сопоставима с радиусом, т. е. R 2= h 2. Соответственно, для оценки критического радиуса тела, которое может начинать заметно отклоняться от сферической формы, получаем:
Читать дальше
Конец ознакомительного отрывка
Купить книгу

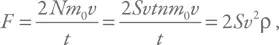
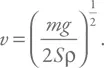
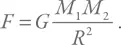
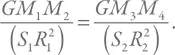
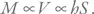 Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.
Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.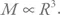 Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение:
Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение: