Чарльз Петцольд - Код. Тайный язык информатики

Чтобы понять, что происходит в этой схеме, давайте посмотрим на функциональную таблицу, иллюстрирующую различные изменения. Допустим, что вход Clk и выход Q равны 0. Значит, выход Q, подключенный к входу D, равен 1.

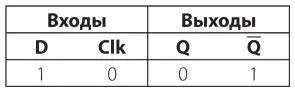
Когда значение входного сигнала Clk изменяется с 0 на 1, выходной сигнал Q становится равным входному сигналу D.

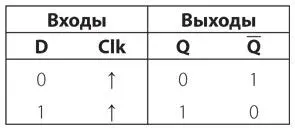
Поскольку выходной сигнализменяется на 0, входной сигнал D также поменяется на 0. Теперь входной сигнал Clk станет равен 1.

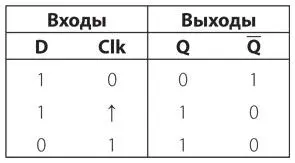
Входной сигнал Clk возвращается к 0, не влияя на значения выходных сигналов.

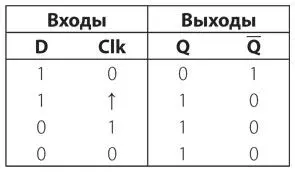
Теперь значение входного сигнала Clk снова изменяется на 1. Поскольку входной сигнал D равен 0, выходной сигнал Q становится равным 0, а выходной сигнал — 1.

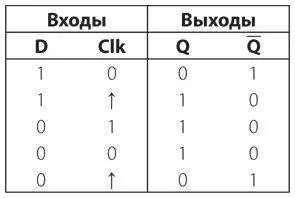
Таким образом, входной сигнал D также становится равным 1.

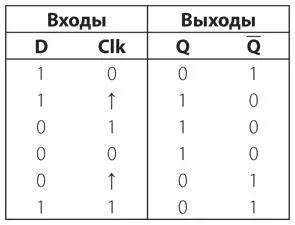
То, что здесь происходит, можно описать очень просто: каждый раз, когда значение входного сигнала изменяется с 0 на 1, значение выходного сигнала Q меняется либо с 0 на 1, либо с 1 на 0. Ситуацию может прояснить следующий график.

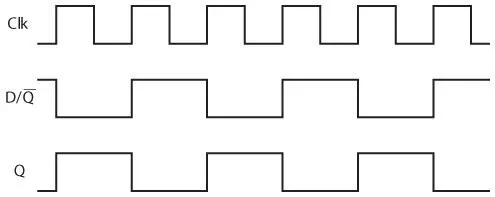
Когда входной сигнал Clk изменяется с 0 на 1, значение на входе D (которое совпадает со значением на выходе Q) передается на выход Q, при этом также изменяется значение Q и D до следующего перехода значения входного сигнала Clk от 0 к 1.

Если частота осциллятора равна 20 герц (20 циклов в секунду), частота выхода Q в два раза меньше — 10 герц. По этой причине такая схема, в которой выход Q соединен со входом триггера «Данные», также называется делителем частоты .

Разумеется, выход делителя частоты может являться входом Clk другого делителя частоты для повторного деления частоты. На следующем изображении показана схема, состоящая из трех делителей частоты.

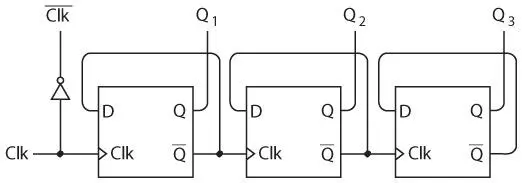
Давайте рассмотрим четыре сигнала, которые я обозначил в верхней части схемы.

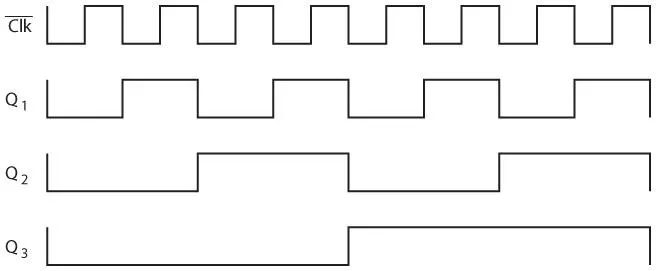
Признаю, что я выбрал самые подходящие точки начала и окончания этой диаграммы, однако ничего нечестного в этом нет: этот шаблон повторяется в данной схеме снова и снова. Не кажется ли она знакомой?

Подскажу: обозначим эти сигналы нулями и единицами.

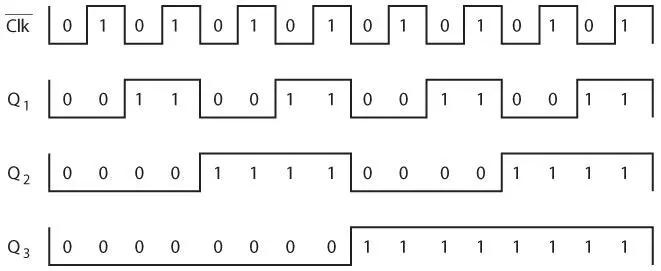
Не догадались? Попробуйте повернуть диаграмму на 90 градусов по часовой стрелке и прочитать 4-битные числа по горизонтали. Каждое из них соответствует десятичному числу от 0 до 15.

Двоичное число

Десятичное число

0000

0

0001

1

0010

2

0011

3

0100

4

0101

5

0110

6

0111

7

1000

8

1001

9

1010

10

1011

11

1100

12

1101

13

1110

14

1111

15

Эта схема производит подсчет в двоичном формате , и чем больше триггеров добавляем в схему, тем большую сумму можно получить с ее помощью. В главе 8 я указал, что в последовательности возрастающих двоичных чисел каждый столбец цифр чередуется между 0 и 1 с частотой вдвое меньшей, чем столбец справа от него. Этот счетчик имитирует эту закономерность. При каждом положительном переходе сигнала Clk значения выходных сигналов счетчика увеличиваются на 1, это и называется приращением или инкрементом .

Давайте объединим восемь триггеров и поместим их в общий корпус.

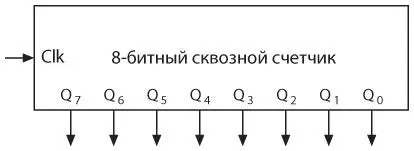
Схема называется сквозным счетчиком , потому что выход каждого триггера становится входом Clk следующего. Изменения сигнала проходят последовательно через все триггеры, а изменения триггеров, находящихся в конце, могут происходить с небольшой задержкой. Более сложные счетчики — синхронные , в них все выходные сигналы изменяются одновременно.