Сергей Струговец - Естественная механика природы. Автореферат книги

Так как материя одномерна и её элементы (кванты) постоянно движутся друг относительно друга, для описания как материи, так и пространства нашего Мира необходимы и достаточны только два фундаментальных измерения – длина и время . Углы в полярных и сферических системах координат не являются самостоятельными измерениями, так как они могут быть выражены через длину (фундаментальное измерение), что отражает единица измерения угла – радиан. Такие фундаментальные физические параметры мироздания, как масса и сила, определяют количественную взаимосвязь между длиной и временем, и воспринимаются нами визуально через эту взаимосвязь.

Примечание. То, что материя нашей Вселенной вообще не имеет собственного объёма, а формирует его в пространстве за счёт объёмной структуры одномерных силовых линий, соединённых между собой в безразмерных точках, может, на первый взгляд, показаться чем-то излишне экзотичным. Однако именно при такой интерпретации материи появляется возможность избавиться от целого ряда гораздо более экзотичных представлений о природе, накопившихся в науке, в том числе и от всех тех, которые сегодня не имеют уже никакого наглядно-механистического смысла. К тому же, одномерность, как средство описания элементов материи (например, в теории струн) или даже всего пространства (как в каузальной динамической триангуляции), широко применяется в современной физике. Так что, в части одномерности, в СКТВ, по сути, нет ничего нового.

Чтобы определить связь силы гравитационного взаимодействия тел с их массой, необходимо и достаточно установить функциональную зависимость между количеством КУ, составляющих тела, и количеством КС, эти тела соединяющих.

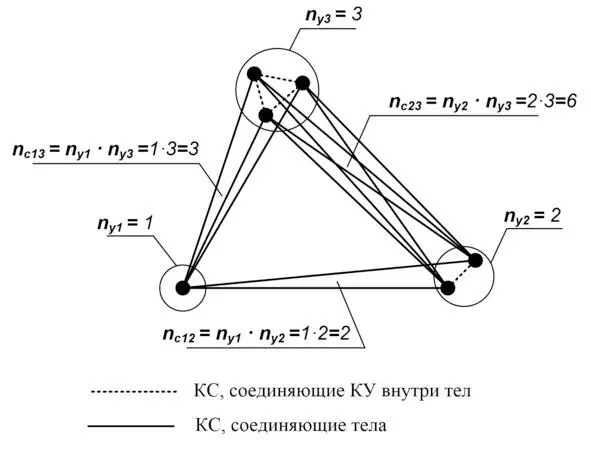
Модель элемента структуры нашей Вселенной, наглядно показывающая зависимость количества КС, соединяющих частицы вещества, от произведения количества КУ, входящих в эти частицы (наглядное объяснение причины произведения инертных масс в законе тяготения).

На рисунке показано, что для любых двух материальных тел в нашей Вселенной, состоящих из, соответственно, n у1 и n у2 узловых квантов, количество соединяющих эти два тела КС ( n c12 ) всегда равно:

Поэтому сила гравитации ( F g ), действующая между двумя телами, расположенными достаточно далеко друг от друга, равна:

где F cg – примерно одинаковая (средняя) сила гравитационного взаимодействия, которую создаёт ГСЛ каждого из связывающих тела соединяющих квантов.

Учитывая связь количества КУ в телах с массой каждого из них ( m у ) и с массой самих тел ( m 1 и m 2 ), получаем:

Отсюда:

Примечание. В формуле F g= G m 1m 2/r 2 , предложенной Ньютоном, произведение масс частиц вещества присутствует явно, а постоянная величина 1 / m у 2 скрыта в коэффициенте G , называемом гравитационной постоянной. То есть хорошо объясняется не только произведение масс в числителе формулы, но и, частично, размерность G (кг 2в знаменателе размерности этого коэффициента, в СИ). Ну, а то, что F cg обратно пропорциональна r 2 – это общий закон для обеих силовых линий соединяющего кванта. Кстати сказать, постулировав несколько иначе понятие «скорость», можно считать, что F cg обратно пропорциональна r 3 . Такая зависимость, как это будет показано ниже, используется в СКТВ для объяснения причин изменения размеров нашей Вселенной по закону Хаббла.

Таким образом, термин «тяжёлая масса» утрачивает свой физический смысл, так как никакой прямой причинно-следственной связи между массой и силой гравитации нет. Размерность «тяжёлой» массы в формуле закона тяготения сокращается, а в размерности силы масса присутствует, согласно второму закону Ньютона, только как инертная. Соответственно, теряет всякий смысл и сложнейший математический аппарат общей теории относительности Эйнштейна, описывающий, как тяжёлая масса искривляет континуум пространства-времени, создавая этим гравитацию.