С тех пор отмеченные тенденции только укрепились. Начиная, как минимум, с К.Шеннона, даже информация обретает свою количественную, дискретную меру, современная техника отдает все большее предпочтение цифровым технологиям.
Означенный процесс алгебраизации и/или арифметизации не обошел стороной и науки о языке (лингвистика Ф. де Соссюра, фонология Н.Трубецкого, семиотика), искусстве ("формальная школа" в литературоведении, структурализм), первобытном мифе и обществе (Леви-Брюль, Леви-Строс и др.). Об этом уже упоминалось в разделе 1.1, но сейчас нас интересует более специальный аспект. Однако прежде – еще одно отступление.
Рассматриваемые системы класса S – будь то из предшествующего раздела или из настоящего – хорошо известны науке и носят в топологии наименование симплексов (от лат. simplex – простой). Прообразом двумерных симплексов служит треугольник, трехмерных – тетраэдр (треугольная пирамида):
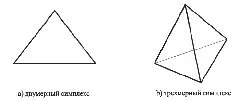
Рис. 1-14
Для изображения тройственных систем (т.е. двумерных симплексов) ранее уже использовались треугольники, в частности треугольник Фреге (рис. 1-6); та же фигура является одним из иконографических символов Троицы. Треугольник способен служить наглядной схемой и для прочих триад.
В качестве элементов (в принятой терминологии) могут быть выбраны вершины треугольника, в качестве отношений между элементами – его стороны. Каждая из сторон соединяет пару вершин, будучи, таким образом, бинарным отношением ( n = 2 ). Каждая из вершин треугольника соединена соответствующими сторонами с каждой, т.е. система связна. Количества вершин и сторон совпадают: М = k, ср. уравнение (1) из раздела 1.2, – каждое из них равно трем.
С ничуть не меньшим основанием можно назначить элементами стороны треугольника; в таком случае роль отношений сыграли бы пересечения сторон, т.е. вершины. Каждое из пересечений, очевидно, бинарно, по-прежнему n = 2. Система в этом плане логически симметрична, инверсивна.
Подобное разложение треугольника не противоречит холистичности его восприятия. Один из исследователей науки напоминает о платоновской традиции целостного, интуитивного постижения геометрических истин: "Хотя треугольник и сложен из отрезков прямых, его свойства не дедуцируются из свойств прямой как таковой. Интуиция треугольника так же неделима, как неделимы слоги в известном рассуждении Платона из "Теэтета"" [152, c. 29], – и далее, ссылаясь на Платона, Аристотеля, Прокла, отмечает наличие и эстетического аспекта.
Если тройственные структуры ассоциируются с двумерными симплексами, то рассматриваемые в настоящем разделе четверичные – с симплексами трехмерными. Тетраэдр – также замкнутый геометрический объект, в котором каждая тройка его вершин соединена соответствующей гранью, т.е. в системе конституированы тринитарные отношения, n = 3. Аналогично предшествующему примеру, в качестве элементов могут быть выбраны вершины, отношений – грани пирамиды, но с равным успехом и наоборот, поскольку любая из вершин представляет собой пересечение трех и именно трех граней. Система по-прежнему логически инверсивна. Числа вершин и граней в тетраэдре совпадают ( М = k ), каждое из них равно четырем.
Помимо двумерных и трехмерных, топология оперирует симплексами произвольной размерности, n – мерными, где n может быть как больше, так и меньше двух или трех. В n – мерном эвклидовом пространстве симплексом называется замкнутая фигура n измерений, обобщающая понятия треугольника и тетраэдра. Пока мы, впрочем, сосредоточили внимание на тройственных и кватерниорных системах, хотя в нашем распоряжении есть и общее решение для различных n, М – выражения (9), (10), – которым отвечают симплексы произвольных размерностей.
В ХХ в. возник такой эффективный раздел математики как комбинаторная топология (см., напр., [258]или [14]). Геометрические объекты произвольной формы разбиваются на простейшие составляющие, симплексы. И наоборот: из последних, как из деталей конструктора, могут быть собраны фигуры произвольной конфигурации. Т.е. не только системы S, симплексы обладают элементарно-комбинаторной природой, но и используя такие системы как готовые блоки, "кирпичи", из них можно строить всевозможные сочетания. Так называемый симплекс-метод применяется, в частности, в экономике.
С середины ХIХ и особенно в ХХ в. наука, культура проявляют все бóльшую склонность к интеллектуальным операциям подобного сорта, воспроизводя тем самым древний алфавитный принцип: слова состоят из слогов, из букв, комбинируя слова, можно составлять фразы, абзацы, текст в целом. (О коррелятивности алфавитного и числового принципов упоминалось в разделе 1.1.) Многообразие химических веществ изображается в форме соединений химических элементов (записываются формулы, для реакций составляются уравнения). С начала ХХ в. сами эти элементы, атомы представляются в виде сочетаний элементарных частиц (теперь утверждают, что и последние могут быть разложены на кварки). Не отставала и биология – учения, разгадывающие генетический код, открыто говорят о четырехбуквенном алфавите А – Г – Т – Ц (если угодно, еще один образец кватернионов ХХ в.). Сходные "блочные" тенденции присущи и технике, логике, культурологии (структурализм) и даже искусству (например, пуантилизм по отношению к цвету, кубизм по отношению к форме, концептуализм применительно к иделогемам, мифологемам, штампам сознания).
Читать дальше
Конец ознакомительного отрывка
Купить книгу












