Дмитрий Гусев - Краткий курс логики - Искусство правильного мышления

Однако если бы понятия « месяц » и « год » были подчинёнными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий « карась » и « рыба »: карась – это обязательно рыба, но рыба – это не обязательно карась). Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия « месяц » и « год », так же, как и понятия « книга » и « страница книги », « автомобиль » и « колесо автомобиля », « молекула » и « атом », находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.

Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причём до сих пор мы изображали схематично отношения между двумя понятиями, но это можно сделать и с большим числом понятий.

Например, отношения между понятиями « боксёр » (Б), « негр » (Н) и « человек » (Ч) изображаются следующей схемой Эйлера (рис. 7).

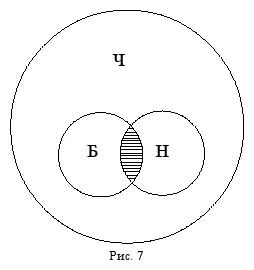
Взаимное расположение кругов показывает, что понятия « боксёр » и « негр » находятся в отношении пересечения: боксёр может быть негром и может им не быть, а негр также может быть боксёром и может им не быть, а понятия « боксёр » и « человек », так же как понятия « негр » и « человек », находятся в отношении подчинения: любой боксёр и любой негр – это обязательно человек, но человек может не быть ни боксёром, ни негром.

Рассмотрим отношения между понятиями « дедушка » (Д), « отец » (О), « мужчина » (М), « человек » (Ч) с помощью схемы Эйлера (рис. 8).

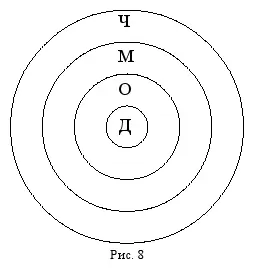
Указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.

Отношения между понятиями « хищник » (Х), « рыба » (Р), « акула » (А), « пиранья » (П), « щука » (Щ), « живое существо » изображаются следующей схемой Эйлера (рис. 9).

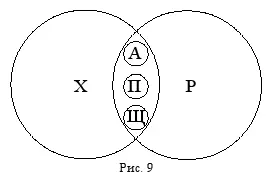
Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.

Подытоживая всё сказанное, отметим, что отношения между понятиями – это отношения между их объёмами. Значит, для того чтобы можно было установить отношения между понятиями, их объём должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определёнными.

1. Какие понятия называются в логике совместимыми, а какие – несовместимыми? Приведите по пять примеров совместимых и несовместимых понятий.

2. В каких отношениях могут быть совместимые понятия? Что представляют собой отношения равнозначности, пересечения и подчинения между понятиями? Что такое видовые и родовые понятия?

3. В каких отношениях могут быть несовместимые понятия? Что представляют собой отношения соподчинения, противоположности и противоречия между понятиями? Чем отличается противоположность от соподчинения и противоречие от противоположности?

4. Каким образом изображаются отношения между понятиями?

5. В каком отношении находятся понятия, обозначающие часть и целое? Почему между этими понятиями не может быть отношения подчинения?

6. Определите, в каких отношениях находятся следующие понятия: двоечник и студент , композитор и человек , город и деревня , Антарктида и ледовый матери к, небесное тело и звезда , треугольник и сторона треугольника , школа №5 и учебное заведение , майор и россиянин , знаменитый человек и немецкий писатель , дом и крыша дома , собака и кошка , умный человек и неумный человек , монарх и самодержец , физика и химия , геометрия и тригонометрия , столица и населённый пункт , книга и интересная книга , телевизор и планета солнечной системы , растение и крапива , окружность и круг , Николай II и последний русский царь , олимпийские игры и спортивные состязания .