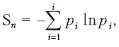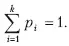Коллектив Авторов - Концепции современного естествознания

Возникновение диссипативных структур носит пороговый характер. Неравновесная термодинамика связала пороговый характер с неустойчивостью. Новая структура всегда является результатом неустойчивости и возникает из флуктуации.

Выдающейся заслугой неравновесной термодинамики является установление того, что самоорганизация присуща не только «живым системам». Способность к самоорганизации является общим свойством всех открытых систем, у которых возможен обмен энергией с окружающей средой. При этом именно неравновесность служит источником упорядоченности.

Этот вывод является основным тезисом для круга идей группы И. Пригожина.

Совместимость второго начала термодинамики со способностью систем к самоорганизации – одно из крупнейших достижений современной неравновесной термодинамики.

Энтропия и вещество. Изменение энтропии в химических реакциях

При повышении температуры растет скорость различных видов движения частиц. Отсюда число микросостояний частиц, а соответственно и термодинамическая вероятность W, и энтропия вещества растут. При переходе вещества из твердого состояния в жидкое увеличивается неупорядоченность частиц и соответственно энтропия (ΔS плавл). Особенно резко растет неупорядоченность и соответственно энтропия при переходе вещества из жидкого состояния в газообразное (AS кипен ). Энтропия увеличивается при превращении кристаллического вещества в аморфное. Чем выше твердость вещества, тем меньше его энтропия. Увеличение атомов в молекуле и усложнение молекул ведет к увеличению энтропии. Энтропия измеряется в Кал/моль·К (энтропийная единица) и в Дж/моль·К При расчетах применяют значения энтропии в так называемом стандартном состоянии, то есть при 298,15 К (25 °C). Тогда энтропию обозначают S 0 298. Например, энтропия кислорода 0 3– S 0 298= 238,8 ед. э., а 0 2– S 0 298= 205 ед. э.

Абсолютные значения энтропии многих веществ являются табличными и приведены в справочниках. Например:

Н 20(ж) = 70,8; Н 20(г) = 188,7; СО(г) = 197,54;

СН 4(r) = 186,19; Н 2(г) = 130,58; НС1(г) = 186,69; НСl(р) = 56,5;

СН 30Н(ж) = 126,8; Са(к) = 41,4; Са(ОН) 2(к) = 83,4; С(алмаз) = 2,38;

С(графит) = 5,74 и т. д.

Примечание: ж – жидкость, г – газ, к – кристаллы; р – раствор.

Изменение энтропии системы в результате химической реакции (Δ S) равно сумме энтропий продуктов реакции за вычетом энтропий исходных веществ. Например:

СН 4+Н 20(г) = С0 + 3Н 2– здесь Δ S 0 298= S 0 co.298+ 3 S 0 H2.298– S 0 H4.298– S 0 H2.298=

197,54 = 3 · 130,58 – 188,19 – 188,7 = 214,39 Дж/моль · К.

В результате реакции энтропия возросла (A S > 0), возросло число молей газообразных веществ.

Информационная энтропия. Энтропия в биологии

Информационная энтропия служит мерой неопределенности сообщений. Сообщения описываются множеством величин x 1 , x 2 x n , которые могут быть, например, словами: p 1 , p 2 …, p n . Информационную энтропию обозначают S n или H u . Для определенного дискретного статистического распределения вероятностей P i используют следующее выражение:

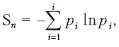
при условии:

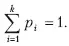
Значение S n = 0, если какая-либо вероятность P i = 1, а остальные вероятности появления других величин равны нулю. В этом случае информация достоверна, то есть неопределенность в информации отсутствует. Информационная энтропия принимает наибольшее значение, когда P i равны между собой и неопределенность в информации максимальна.

Общая энтропия нескольких сообщений равна сумме энтропий отдельных сообщений (свойство аддитивности).

Американский математик Клод Шеннон, один из создателей математической теории информации, использовал понятие энтропии для определения критической скорости передачи информации и при создании «помехоустойчивых кодов». Такой подход (использование из статистической термодинамики вероятностной функции энтропии) оказался плодотворными в других направлениях естествознания.

Понятие энтропии, как показал впервые Э. Шредингер (1944 г.), а затем Л. Бриллюэн и др., существенно и для понимания многих явлений жизни и даже деятельности человека.

Теперь ясно, что с помощью вероятностной функции энтропии можно анализировать все стадии перехода системы от состояния полного хаоса, которому соответствуют равные значения вероятностей и максимальное значение энтропии, к состоянию предельно возможной упорядоченности, которому соответствует единственно возможное состояние элементов системы.