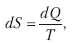Коллектив Авторов - Концепции современного естествознания

Второе начало термодинамики вводит в рассмотрение новую функцию состояния – энтропию. Термин «энтропия», предложенный Р. Клаузиусом, образован от греч. entropia и означает «превращение».

Уместно будет привести понятие «энтропия» в формулировке А. Зоммерфельда: «Каждая термодинамическая система обладает функцией состояния, называемой энтропией. Энтропия вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния в соответствующее конечное состояние через последовательность состояний равновесия; вычисляются все проводимые при этом к системе порции тепла dQ, делятся каждая на соответствующую ей абсолютную температуру Т, и все полученные таким образом значения суммируются (первая часть второго начала термодинамики). При реальных (неидеальных) процессах энтропия изолированной системы возрастает (вторая часть второго начала термодинамики)».

Учета и сохранения количества энергии еще недостаточно для того, чтобы судить о возможности того или иного процесса. Энергию следует характеризовать не только количеством, но и качеством. При этом существенно, что энергия определенного качества самопроизвольно может превращаться только в энергию более низкого качества. Величиной, определяющей качество энергии, и является энтропия.

Процессы в живой и неживой материи в целом протекают так, что энтропия в замкнутых изолированных системах возрастает, а качество энергии понижается. В этом и есть смысл второго начала термодинамики.

Если обозначить энтропию через S,то

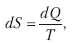
что и соответствует первой части второго начала по Зоммерфельду.

Можно подставить выражение для энтропии в уравнение первого начала термодинамики:

dU = T × dS – dU.

Эта формула известна в литературе как соотношение Гиббса. Это фундаментальное уравнение объединяет первое и второе начала термодинамики и определяет, по существу, всю равновесную термодинамику.

Второе начало устанавливает определенное направление течения процессов в природе, то есть «стрелу времени».

Наиболее глубоко смысл энтропии вскрывается при статической оценке энтропии. В соответствии с принципом Больцмана энтропия связана с вероятностью состояния системы известным соотношением

S = K × LnW,

где W – термодинамическая вероятность, а К – постоянная Больцмана.

Под термодинамической вероятностью, или статическим весом, понимается число различных распределений частиц по координатам и скоростям, соответствующих данному термодинамическому состоянию. При любом процессе, который протекает в изолированной системе и переводит ее из состояния 1 в состояние 2, изменение Δ W термодинамической вероятности положительно или равно нулю:

ΔW = W 2– W 1≥ 0

В случае обратимого процесса ΔW = 0, то есть термодинамическая вероятность, постоянна. Если происходит необратимый процесс, то Δ W > 0 и W возрастает. Это означает, что необратимый процесс переводит систему из менее вероятного состояния в более вероятное. Второе начало термодинамики является статистическим законом, оно описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему, то есть энтропия характеризует меру беспорядочности, хаотичности частиц в системе.

Р. Клаузиус определил второе начало термодинамики так:

► невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому (1850).

В связи с этой формулировкой в середине XIX в. была определена проблема так называемой тепловой смерти Вселенной. Рассматривая Вселенную как замкнутую систему, Р. Клаузиус, опираясь на второе начало термодинамики, утверждал, что рано или поздно энтропия Вселенной должна достигнуть своего максимума. Переход теплоты от более нагретых тел к менее нагретым приведет к тому, что температура всех тел Вселенной будет одинаковой, наступит полное тепловое равновесие и все процессы во Вселенной прекратятся – наступит тепловая смерть Вселенной.

Ошибочность вывода о тепловой смерти Вселенной заключается в том, что нельзя применять второе начало термодинамики к системе, которая является не замкнутой, а бесконечно развивающей системой. Вселенная расширяется, галактики разбегаются со скоростями, которые нарастают. Вселенная нестационарна.