Дмитрий Гусев - Удивительная логика

Примеры делений с пересечением результатов:

Художественные романы бывают приключенческими, детективными, фантастическими, историческими, любовными и другими.

Спортивные состязания бывают мировыми, международными, олимпийскими и другими.

По темпераменту люди делятся на сангвиников, меланхоликов, флегматиков и холериков.

4. Деление должно быть последовательным,т. е. не допускающим пропусков и скачков. Рассмотрим следующее деление: Леса бывают хвойными, лиственными, смешанными и сосновыми. Явно лишним здесь выглядит понятие сосновые леса, в силу чего допущенная в делении ошибка напоминает подмену основания. Однако основание в данном случае не менялось: деление было проведено по одному и тому же основанию – тип древесных листьев. Правильно было бы разделить леса на хвойные, лиственные и смешанные, а потом произвести второе деление – разделить хвойные леса на сосновые и еловые. Таким образом, надо было совершить два последовательных деления, а в приведенном примере второе деление пропущено, через него как бы перескочили, в результате чего два деления смешались в одно. Такая ошибка называется скачком в делении. Еще раз отметим, что скачок в делении не следует путать с подменой основания. Например, в делении Учебные заведения бывают начальными, средними, высшими и университетами присутствует скачок, а в делении Учебные заведения бывают начальными, средними, высшими и коммерческими допущена подмена основания.

Примеры делений, в которых присутствует скачок:

Геометрические фигуры делятся на плоские, объемные, треугольники и квадраты.

Учащиеся бывают успевающими, отстающими и отличниками.

Преступления делятся на умышленные, неумышленные и квартирные кражи.

Помимо рассмотренных нами логических операций ограничения, обобщения, определения и деления понятия, существуют еще две важные операции. Это сложение и умножение понятий.

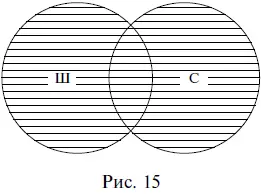
Сложение понятий– это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой (рис. 15).

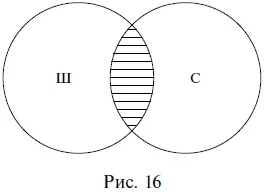
Умножение понятий– это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (рис. 16).

Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения: школьник и спортсмен. При других отношениях между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Результаты сложения понятий, при сравнении их с результатами умножения, полностью совпадают только в случае равнозначности, частично совпадают в пересечении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а результатом умножения – видовое.

Как правило, в естественном языке (том, на котором мы общаемся) результат сложения понятий выражается союзом ИЛИ, а умножения – союзом И. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является ИЛИ школьником, ИЛИ спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является И школьником, И спортсменом одновременно.