А Александров - Числа и съдби (Ключ към разбиране на миналото, настоящето и бъдещето)

Една цифра. Върху плоскостта е определена една-единствена точка А (фиг. 2).

Фиг. 2

Фактът, че точката А е единствена, я прави уникална или открояваща се върху плоскостта и точно това характеризира качествата, зададени от едната цифра, като слаби, но стремящи се към открояване и показване, сякаш единствената точка е много слаба, но е една-единствена върху плоскостта. Геометрично това отговаря на нулева размерност dim = 0 (точката върху плоскостта). Интересно е, че нулевата размерност още по-ясно показва слабостта на качеството, зададено от една цифра.

Две цифри. Върху плоскостта са зададени две точки А и В, които неизбежно задават правата АВ или ВА в зависимост от началната точка (фиг. З).

Фиг. 3

Особеностите на правата се изразяват в това, че тя еднозначно определя посоката на движение, което говори за определеност и конкретност на пътя. За качествата, характеризиращи се с две цифри, това ще означава естествена норма: появява се необходимост от проявяване на едно или друго качество и човек го прави свободно. От геометрична гледна точка имаме едноизмерно пространство dim=1, което още веднъж подчертава еднозначността във възможността за използване на качеството.

Три цифри. Както знаем, три точки образуват конкретна плоскост, но в нашия случая по-важното е, че те определят една площ S, която е ограничена от периметъра на триъгълника АВС (фиг. 4).

Фиг. 4

Особеното в случая е, че от всеки връх на триъгълника можем да наблюдаваме две равнозначни посоки към другите два върха, което създава затруднение при избора на последователност в движението към един от върховете на фигурата. Точно същите затруднения в проявата на конкретното качество изпитва и човек, когато даденото качество е зададено от три цифри. Той сякаш изчаква външно «нападение» или промяна, която еднозначно да определи избора на движението. Можем да кажем, че човек проявява качеството си само когато не му остава избор и трябва да действа. Нека отбележим, че силата на проява на качеството рязко нараства, защото имаме значително засилване на качеството, отразено чрез площта S на триъгълника АВС. Щом човек изразходва качеството (целия му запас), той отново ще чака екстремална ситуация, когато отново може да «изригне запасите от качеството». Интересното е, че за целта ще трябва да натрупа сили за подобна ненадейна и силна проява на въпросното качество. От геометрична гледна точка ние разглеждаме едно двуизмерно пространство dim=2, което характеризира плоскостите и площите на фигурите.

Четири цифри. В дадения случай се налага да излезем извън границите на плоскостта, понеже само тогава ще можем качествено да променим ситуацията, а не да задаваме нова плоска фигура (фиг. 5а, б).

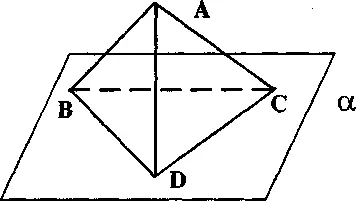
Както добре виждате от фиг. 5, в случай «б» има плоска фигура, която ни връща към предишния случай, когато качеството се задава от плоскостта или dim=2. В случай «а» положението рязко се променя, понеже се появява нова размерност dim=3 (триизмерно пространство). От точка А (върха на пирамидата) виждаме целия триъгълник на основата BCD, което до известна степен прави ситуацията подобна на случая с двете точки върху плоскостта, които определят права та АВ. Точно затова случаят с четирите цифри е също толкова стабилен при проявяването на качеството си, както и при двете цифри. Разликата е само, че силата на самото качество рязко нараства до обема на пирамидата V.

Пет цифри. Тъй като в предишния случай вече засегнахме максималната за човека размерност dim=3 (триизмерното пространство), в случая с петте точки ще ни е много трудно да намерим качествено ново решение, но ще се помъчим да го направим. Както знаем, в геометрията съществува теорема, според която всеки 5 (пет) произволно взети върху дадена плоскост точки определят една-единствена крива от втори ред (1 — окръжност, 2 — елипса, 3 — парабола, 4 — хипербола и няма да разглеждаме всички случаи на трансформиране на кривата). Ще отбележим, че наличието тъкмо на пет точки ни позволява да използваме дадената теорема (фиг. 6).

Фиг. 6

За да илюстрирате тази теорема, можете да вземете произволни пет точки върху дадена плоскост и като помислите малко, доста лесно ще можете да определите коя от посочените криви преминава през взетите от вас точки — за да не по паднете в случай на трансформирана крива от втори ред, не слагайте три и повече точки върху една права, защото в такъв случай линията ще трябва да се трансформира в точка, в две пресечни, успоредни или съвпадащи прави (една права).