Проблема равного темперирования — самая существенная для этой физики и ее инженерных приложений.
Сейчас мы делим музыкальную октаву на двенадцать равных частей со значением 12√2. Это равное темперирование дает следующую гамму [321] Все диаграммы принадлежат Маклейну.
:
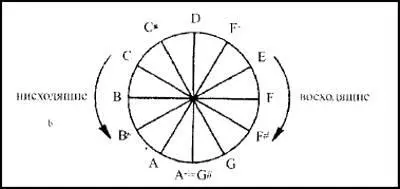
Рис. 1. Гамма с равным темперированием
Однако музыканты знают, что октава с соотношением 1:2 не делится по коэффициенту рациональных чисел, так как степени четных чисел (2, 4, 8 и т. д.), определяющие октавы, никогда не совпадают со степенями тройки (9, 27, 81 и т. д.), определяющими интервалы в одну пятую и одну четвертую. Кроме того, ни одна из этих обертоновых серий не совпадает со степенями числа 5, определяющими интервалы в одну третью. Циклическое совпадение или объединение этих трех обертонных серий может быть достигнуто лишь за счет намеренного искажения интервалов на основе приближения к 12√2. Таким образом, равное темперирование является первым известным примером «объединения полей» в теоретической физике. В данном случае это информационные поля, образованные тремя обертонными сериями октав, пятых, четвертых и третьих. Следует отметить, что такое объединение было достигнуто с помощью инженерии, т. е. путем намеренного искажения и приближения к чистым соотношениям абсолютной математической и физической теории. Без аппроксимации эти соотношения привели бы к «гармоническому хаосу» бесконечного количества обертонов по отношению к основному тону [322] McClain, op.cit., p. 4.
. В свою очередь, это дает ключ к пониманию, как высокая палеоцивилизация могла достигнуть объединения физических принципов.
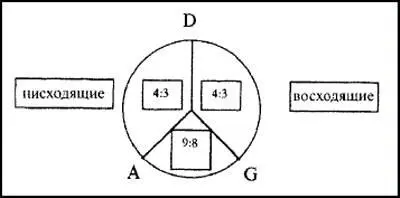
Основой равного темперирования, зашифрованного в текстах Платона, является гармоническая пропорция, которую Пифагор предположительно принес в Грецию из Вавилона. Эта пропорция выглядела следующим образом:
6:8::9:12.
Если взять эту пропорцию для определения промежутка октавы, она имеет два средних значения: арифметическое среднее Ма = 1 ½ и гармоническое среднее Mh= 1 1/3.

Эти свойства применимы как к восходящей, так и к нисходящей последовательности:

Платон утверждает:
(Законодатель) должен принять как общее правило, что численное деление во всем его разнообразии может быть с пользой применено во всех областях деятельности. Оно может быть ограничено сложностями самой арифметики или распространено на тонкости плоскостных и объемных геометрических тел; оно также применяется к звукам и движению, по восходящей, по нисходящей или по окружности [323] Платон, «Законы», 747а, цит, по: McClain, р. 10.
.
По сути дела, Платон сказал поразительную вещь: каждая область человеческой деятельности или исследований доступна для математического моделирования. Таким образом, физика может быть арифметически и математически промоделирована, и эта модель определяется арифметическими, гармоническими и геометрическими средствами.
Обратимся к рассмотрению одного из самых важных компонентов анализа Маклейна, загадочному платоновскому «верховному числу» — 60 4, или 12 960 000. Маклейн отмечает, что в платоновских гармониках это число выполняет функцию «тонального индекса», т. е. «произвольного окончания потенциально бесконечной генерации тональных чисел; ограничения, которое (sic) предоставляет целочисленные выражения для некоторого набора пропорций» [324] McClain, op.cit, p. 17.
.
Однако в этом числе нет ничего произвольного, поскольку оно одновременно делится на гармоники постоянной Планка, длины Планка и массы Планка в пределах одного десятичного знака. Если взять численные значения этих величин с точностью до третьего знака после запятой и перевести метрические меры в английские (так как последние очень близки к единицам измерения Великой Пирамиды), можно получить следующие значения планковских единиц:
| Планковская единица |
Теоретическая величина |
Гармоническое число |
| h (постоянная Планка) |
6,626x10 -34джоулей |
6626 2 |
| L (длина Планка) |
6,362x10 -8дюймов |
6362 |
| M p(масса Планка) |
4,799x10 -8 |
4799 [325] Теоретическая величина постоянной Планка 6,626076 х 10 -34 джоулей. |
Разделив «верховное число» 12 960 000 на гармонические числа единиц Планка, мы получаем поразительный результат:
Читать дальше















