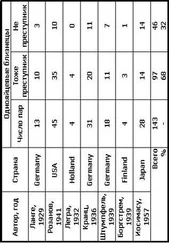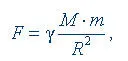
где γ = 6,7 10 -11м 3/(кг • с 2) – гравитационная постоянная; m 1и m 2– массы тел; r – расстояние между телами.
7. ПРИНЦИПЫ ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
Во всех инерциальных системах отсчета законы классической механики (законы Ньютона) имеют одинаковую форму; в этом сущность механического принципа относительности – принципа относительности Галилея.Он означает, что уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т. е. инвариантны по отношению к преобразованиям координат.
x ′ = x – vt , y ′ = y , z ′ = z , t ′ = t ,
где x , y , z и t ; x ′, y ′, z ′ и t ′– координаты тела и время в неподвижной и подвижной системах отсчета соответственно; v – скорость подвижной системы отсчета.
Эти формулы называются преобразованиями Галилея.
Легко показать, что законы динамики Ньютона инвариантны относительно преобразований Галилея. Это объясняется тем, что силы и массы тел одинаковы во всех инерциальных системах отсчета и ускорения тел, которые определяются двойным дифференцированием координат по времени, также одинаковы
(a = d 2 x/dt 2= d 2x'/dt 2= a').
Инвариантами, т. е. величинами, численное значение которых не изменяется при преобразовании координат по Галилею, являются длины и интервалы времени. Покажем это.
Пусть в подвижной системе координат находится неподвижный стержень, координаты концов которого (x´ 1 , y 1´ , z´ 1 ) и (x´ 2 , y´ 2 , z´ 2 ). Это означает, что длина стержня в подвижной системе
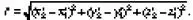
Тогда относительно неподвижной системы отсчета стержень движется поступательно и все его точки имеют скорость v. Длиной движущегося стержня, по определению, называется расстояние между координатами его концов в некоторый момент времени. Таким образом, для измерения длины движущегося стержня необходимо одновременно, т. е. при одинаковых показаниях часов неподвижной системы отсчета, расположенных в соответствующих точках, отметить положение концов стержня. Пусть засечки положения концов движущегося стержня сделаны в неподвижной системе координат в момент времени t и характеризуются координатами (х 1, у 1, z 1) и (х 2, у 2, z 2). Тогда для длины стержня в неподвижной системе отсчета будем иметь
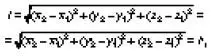
т. е. длина стержня в обеих системах координат одинакова. Это позволяет утверждать, что длина является инвариантом преобразований Галилея.
8. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
В 1904 году Лоренц предложил формулы для преобразования координат, которые обеспечивают инвариантность уравнений Максвелла при переходе от одной инерциальной системы отсчета к другой:
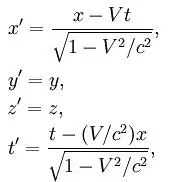
где с – скорость света в вакууме.
Формулы были названы Пуанкаре преобразованиями Лоренца.
Инвариантным относительно преобразований Лоренца является так называемый пространственно-временной интервал, или просто интервал. Пусть события произошли в точке х 1, у 1, z 1в момент времени t 1и в точке х 2, у 2, z 2в момент времени t 2. Интервалом между событиями, или, как говорят, интервалом между точками х 1, у 1, z 1, t 1и х 2, у 2, z 2, t 2, называется величина s, квадрат которой определяется формулой
S 2= С 2(t 2– t 1) 2– (Х 2– Х 1) 2– (У 2– У 1) 2– (Z 2– Z 1) 2. (1)
В подвижной системе отсчета квадрат интервала S записывается в виде
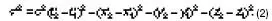
Подставляя формулу (1) в (2), убедимся, что s 2= s' 2= inv. Впервые понятие интервала ввел Пуанкаре, и он же показал, что интервал является инвариантом при преобразованиях Лоренца.
Из преобразований Лоренца следует сокращение длины движущегося стержня, а именно 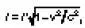 где l = x 2 – x 1и l ' = x' 2– x1, и замедление хода движущихся часов, а именно
где l = x 2 – x 1и l ' = x' 2– x1, и замедление хода движущихся часов, а именно 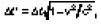 ,где Δt = t 2– t 1 и Δ t' = = t' 2-t' 1.
,где Δt = t 2– t 1 и Δ t' = = t' 2-t' 1.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

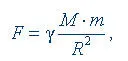
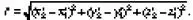
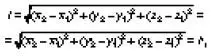
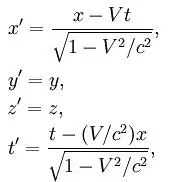
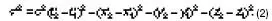
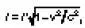 где l = x 2 – x 1и l ' = x' 2– x1, и замедление хода движущихся часов, а именно
где l = x 2 – x 1и l ' = x' 2– x1, и замедление хода движущихся часов, а именно 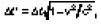 ,где Δt = t 2– t 1 и Δ t' = = t' 2-t' 1.
,где Δt = t 2– t 1 и Δ t' = = t' 2-t' 1.