Владимир Гетман - Внуки Солнца

Решено было дар принять. Так гигантский конь оказался в самом сердце Трои, на городской площади. Нескончаемым потоком до самой темноты ходили вокруг него восхищенные троянцы. Наконец город затих. Троя видела свой последний сон. Глубокой ночью гигантское чрево коня распахнулось, и сорок десантников, перебив охрану, отомкнули ворота и впустили в город греческих завоевателей. Троя бнла разрушена…

Вот такая сказочная, хотя и печальная история. А может, и не история вовсе, а выдумка. Может быть, не было никакого Троянского коня, да и самой Трои никогда не было? Мало ли что можно придумать.

Но вот в 1870 году при раскопках холма Госсарлык немецкий археолог Генрих Шлиман обнаружил древнюю Трою. Исследования показали, что около 1260 года до н. э. Троя находилась в продолжительной осаде и в конце концов была разрушена до основания. Так что великий Гомер познакомил нас с историческим фактом…

Но вернемся к астероидам. Группа Ахилла, в которую входят астероиды Агамемнон, Аякс, Гектор, Диомед, Нестор, Одиссей и другие «греки», так и названа «греками». Вторая группа с Анхизом, Патроклом, Приамом, Энеем и множеством других названа «троянцами».

Взгляните на рис. 4. Не правда ли, изящная картинка? В центре Солнце, вокруг него орбиты Марса и Юпитера, и ровно на 60° по ту и другую сторону от самого Юпитера расположились два «враждующих» лагеря. Вот такой вереницей «греки» — Юпитер — «троянцы» и движутся по одной и той же орбите вокруг Солнца. При этом Юпитер выполняет великую миротворческую миссию, не давая сблизиться двум «армиям» и затеять повторную истребительную «Троянскую войну».

Шутки шутками, а удивительная правильность небесного ромба (рис. 4) просто поражает! Какая тонкая закономерность лежит в основе этой геометрии? Доступна ли она нашему пониманию? Ведь посмотрите, и «греки» и «троянцы» находятся в вершинах двух правильных треугольников. Почему?

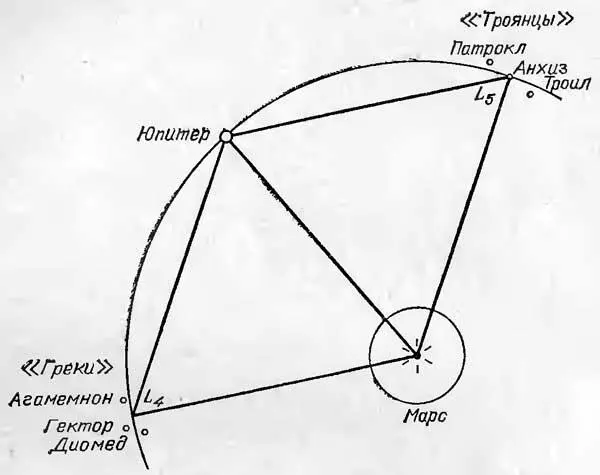
Рис. 4. Изумительный по своей правильности небесный ромб? Солнце — «греки» — Юпитер — «троянцы»

В начале XVII века немецкий астроном Иоганн Кеплер установил три закона движения планет, носящие его имя. Формулировка их удивительно проста и лаконична:

1) каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце;

2) радиус-вектор планеты в равные промежутки времени описывает равновеликие площади;

3) квадраты времен обращения планеты вокруг Солнца (квадраты периодов) относятся как кубы больших полуосей орбит.

Фундаментальная глубина этих законов была до конца понята на основе закона всемирного тяготения, открытого Исааком Ньютоном.

Внешняя простота законов Кеплера была обусловлена тем, что они описывали взаимодействие только двух тел, а именно Солнца и планеты, без учета влияния остальных тел Солнечной системы, поскольку это влияние для таких случаев чрезвычайно мало.

Однако если рассматривать движение астероида вокруг Солнца, то может оказаться, что влияние таких «важных лиц» Солнечной системы, как гигант Юпитер, окажется существенным. В таком случае для описания движения астероида необходимо рассматривать взаимодействие трех тел: Солнца, Юпитера и астероида. В небесной механике подобное рассмотрение называется решением задачи трех тел.

Еще за полвека до открытия первого астероида французский астроном Жозеф Лагранж исследовал некоторые особые варианты задачи трех тел, в частности Солнца, планеты и малого тела. Ему удалось выявить поразительную закономерность, а именно: в системе трех тел, связанных друг с другом силами тяготения, существуют пять точек, в которых силы, действующие на малое тело, уравновешиваются.

Может ли такая закономерность быть справедливой для случая астероидов? Может. Из исследования Лагранжа вытекает, что если первое тело имеет крошечную массу по сравнению с массами двух других тел, а масса второго меньше 0,04 массы третьего тела, то все они будут вращаться вокруг общего центра масс, и при этом их расположение друг относительно друга останется неизменным. Это условие в нашем случае соблюдается с избытком: массы астероидов ничтожны по сравнению с массами планет, а масса Юпитера составляет 0,001 массы Солнца.

Итак, «троянцы» находятся в двух из пяти лагранжевых точек, L 4 и L 5 , являясь вершинами равносторонних треугольников, у которых в двух остальных вершинах расположены Солнце и Юпитер. Каждая сторона этих гигантских треугольников составляет 5,2 астрономические единицы или 780 миллионов километров!