Владимир Гетман - Внуки Солнца

Давайте подставим в формулу вместо n единицу и получим, что для Земли

r n = 1.

С помощью калькулятора вы можете посчитать расстояния для остальных планет. Не исключаю, что «такой пустяк» можно посчитать и в уме. Пожалуйста. Если не ошибетесь, то по результатам можете составить небольшую таблицу (см. табл. 1).

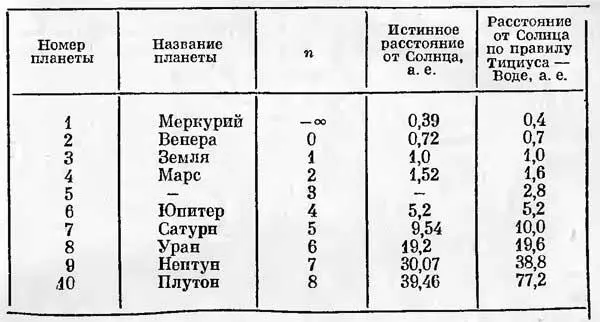
Таблица 1.

Впрочем, если вы решили считать в уме, то можно воспользоваться и другим, может быть, для некоторых более подходящим способом.

Пронумеруйте планеты, против каждого номера напишите цифру 4, а затем прибавьте к первой 0, ко второй 3, к третьей 6, затем 12, 24 и т. д. Каждую сумму разделите на 10 (см. табл. 2).

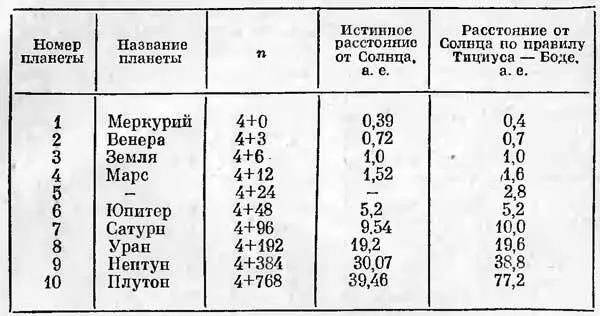
Таблица 2.

Беглого взгляда достаточно, чтобы убедиться, что, во-первых, для планеты под номером 5 нет истинного расстояния, да, собственно, и самой планеты нет, и, во-вторых, что-то непонятное происходит с Нептуном и Плутоном.

Мы уже говорили, что правило Тициуса — Боде — это не закон, подобный, например, законам Кеплера или Ньютона, а правило, которое было получено из анализа имеющихся данных о расстояниях планет от Солнца. Просто некое удивительное соотношение, мимо которого проходили долгое время. Никакого теоретического обоснования правило Тициуса — Боде не имеет. Конечно, отклонения от правила вполне естественны. Во всяком случае, их можно было ожидать. Самые серьезные отклонения проявляются по отношению к Нептуну и Плутону.

Но зато для других планет совпадение просто фантастическое!

Вы вправе задать вопрос: «А почему нет названия у пятой планеты и где она сама?» Когда Боде обнародовал правило в 1772 году, Уран, Нептун и Плутон еще не были открыты астрономами. И представьте себе, в 1781 году открывают Уран, и оказывается, что для него имеет место хорошее совпадение с правилом Тициуса — Боде! Именно оно подтолкнуло астрономов к поиску пятой планеты между орбитами Марса и Юпитера. Хотя при этом возникало немало споров. Широкое обсуждение вопроса состоялось на Астрономическом конгрессе в 1796 году. Дело новое, а поэтому не все его одобряли.

Конечно, не всякое новое бывает действительно достойно этого определения, но даже безусловно новое часто завоевывает себе «место под Солнцем» в трудных боях. А случай правила Тициуса — Боде как раз нельзя было считать на сто процентов достоверным, и поэтому не стоит удивляться, что часть астрономов была весьма скептически настроена по этому поводу. Случайное совпадение и не более!

К нашему сожалению, стенограмма этой дискуссии не сохранилась, но мы можем насладиться поучительным примером, как оптимистам удалось сломить скептиков.

Как бы то ни было, но «недостающую» планету в пространстве между Юпитером и Марсом стали искать.

Я не знаю, чью сторону в этом споре взяли вы, дорогой читатель, но хотелось бы видеть вас среди оптимистов. Пока вы молоды, вас должны обуревать приступы фантазии и тяга к поиску.

Но это к слову. Вернемся к нашей истории. Астрономы приступили к поиску пятой планеты.

А, кстати, как бы вы повели себя на их месте, берясь за новое дело?

Не думаю, что «безропотно» наводили бы телескопы в предполагаемые области неба и ночи напролет молча обшаривали его градус за градусом. Наверняка бы при этом ворчали:

— Почему же эту планету еще никто никогда не видел? Предполагаемое расстояние ее от Солнца составляет около трех астрономических единиц, т. е. примерно 420 миллионов километров, а планеты не видно. А ведь Юпитер отстоит от Солнца на 780 миллионов километров, Сатурн — на 1 миллиард 400 миллионов, а Уран — почти на 3 миллиарда километров! Эти далекие планеты мы видим, а находящуюся, можно сказать, рядом до сих пор не заметили!

В чем дело?

Постой, постой, а может быть, она «слеплена» из другого «теста», и поэтому ее поверхность очень скупо отражает солнечный свет?

Но тогда, значит, эта планета не похожа на другие? Почему?

А может быть, она имеет такую угловатую форму и повернута к нам всегда такой неудобной стороной, что весь отраженный свет «стреляет» мимо Земли? Ведь вот «заупрямилась» же Луна, не показывает нам свою обратную сторону. А может быть, Марс загораживает ее от нашего взора?

Да нет, что за чушь? При чем здесь Марс? Здесь что-то другое. Но что?