Дмитрий Поспелов - Моделирование рассуждений. Опыт анализа мыслительных актов

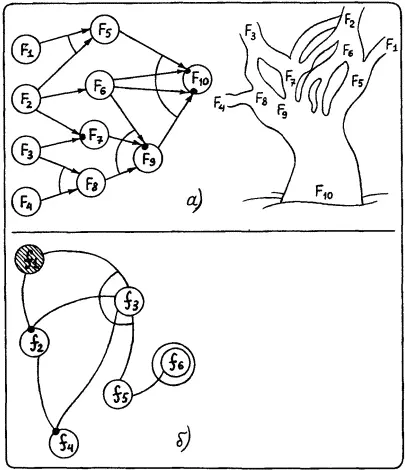
Рис. 19.

Дерево вывода с такими условиями переходов от вершины к вершине носит название И-ИЛИ дерева . В И-ИЛИ дереве ориентация дуг показывает направление вывода. Естественное разбиение вершин дерева по ярусам отражает глубину вывода (число шагов, необходимых для получения утверждений данного яруса). Первый ярус дерева образуют вершины (на рис. 19, а это вершины F 1, F 2, F 3, F 4), играющие роль аксиом или утверждений, истинность которых задается извне.

Схема вывода не обязательно описывается в виде дерева. Она может иметь вид произвольной сети, ориентированной, неориентированной или частично ориентированной. На рис. 19, б показан пример неориентированной сети. Такая сеть (наличие или отсутствие ориентации не играет здесь роли) называется И-ИЛИ сетью . Процесс вывода на И-ИЛИ сети протекает следующим образом. Пусть мы хотим доказать утверждение ? 6(на рис. 19, б этому соответствует целевая вершина ). В качестве априорно доказанного задано утверждение ? 1(ему соответствует начальная вершина, которая на рис. 19, б заштрихована). Как из ? 1можно получить ? 6? Если считать, что все связи допускают ориентацию в нужную сторону, то из ? 1можно получить ? 3, затем ? 5и, наконец, ? 6. Но этот путь нам удалось отыскать потому, что сеть, показанную на рис. 19, б , мы видим «с птичьего полета». Лабиринт поиска лежит в виде чертежа перед нами. Именно это позволяет нам не делать лишних попыток, не двигаться в ненужную сторону, а идти кратчайшим путем к цели.

Подобная ситуация приятна, но редко встречается в действительности. При решении любой задачи, даже если заранее известен ее ответ, к которому надо стремиться (для школьника эта ситуация с подглядыванием в ответ до решения задачи весьма типична), мы не видим перед собой полного лабиринта возможностей. Мы пытаемся построить этот лабиринт, видя лишь начальные «площадки лабиринта» и не зная, что лежит между ними и «целевыми площадками». В нашем примере мы стоим на начальной площадке, в вершине ? 1, и не знаем, куда идти. Мы делаем попытку перейти в ? 2(т.е. вывести утверждение), но видим, что этого нельзя сделать. Тогда мы движемся в сторону утверждения ? 3и обнаруживаем, что его доказательство возможно. Теперь в нашем распоряжении две площадки лабиринта: ? 1и ? 3. Из ? 3можно двигаться в четырех направлениях. Одно из них, ведущее назад к ? 1, интереса не представляет. Попытка продвинуться к ? 2и ? 5оказывается успешной. Возникает новый фронт достигнутых площадок (доказанных утверждений). Теперь его образуют ? 2, ? 3и ? 5. Площадка ? 1исключается из активного фронта, так как использованы все связи этой площадки с другими площадками лабиринта. На следующем шаге достигаются площадки ? 4и ? 6. Наличие среди доказанных выражений целевого ? 6позволяет завершить процесс доказательства. После этого можно произвести «чистку», в результате которой останется лишь тот путь, который кратчайшим образом приводит от начального утверждения ? 1к целевому ? 6.

На примере мы описали процедуру, которая, как легко видеть, носит универсальный характер и пригодна для поиска пути вывода в лабиринтах произвольного типа. Эта процедура известна среди специалистов под названием метода прямой волны . Волна поиска путей к целевой площадке распространяется от всех площадок, играющих роль начальных.

Возможен и другой способ поиска доказательства. Он носит название метода обратной волны . В этом методе волна начинает свое движение от целевых площадок и движется в направлении начальных площадок лабиринта. Для нашего случая на первом шаге была бы порождена площадка, соответствующая ? 5, вслед за этим ? 3и ? 1. На этом движение волны прекратилось бы, так как ее фронт достиг всех (в данном случае единственной ? 1) начальных площадок.

Различие между прямой и обратной волной состоит в том, что они порождают в процессе своего движения различные промежуточные «фронты» площадок, что приводит к различному числу шагов при поиске. Часто используется смешанный метод вывода, при котором одновременно движутся прямая и обратная волны. При встрече этих волн формируется путь вывода от начальных аксиом к целевым выражениям.

Несколько иной разновидностью схем вывода являются так называемые альтернативные деревья или альтернативные сети . В этих схемах выбор дальнейшего пути движения зависит от того, достигнут или не достигнут вывод некоторого выражения. Другими словами, попытки продвижения по лабиринту, которые мы демонстрировали на методе прямой волны при удачах и неудачах, могут влиять на стратегию дальнейшего движения. Такие схемы вывода мы более подробно рассмотрим в пятой главе. Здесь же лишь проиллюстрируем рассуждение такого типа на примере.