Дмитрий Поспелов - Моделирование рассуждений. Опыт анализа мыслительных актов

После нахождения такой пары она передается в блок формирования заключения. В этом блоке проверяется возможность вывода, т.е. возможность того, что пара типов посылок в данной фигуре силлогизма образует правильный модус. Если правильный модус не образуется, то вырабатывается требование на поиск новой пары посылок. Если же вывод возможен, то его результат сравнивается с высказыванием, являющимся целью доказательства теоремы. Если полученное заключение есть искомое высказывание, то процесс доказательства обрывается и результат, говорящий о том, что теорема верна, выдается из системы. Если этого не произошло, то полученное заключение добавляется в базу фактов и процесс поиска доказательства продолжается.

В рассмотренной процедуре возникает проблема остановки. Если нужный факт не выводится из той системы посылок, которая имеется в базе фактов, то как это узнать? Единственный возможный ответ связан с полным перебором всех сочетаний посылок, дающих фигуры силлогизма. Это же касается и случая прекращения процесса пополнения базы фактов после введения нового факта в систему.

Суммируя все сказанное, необходимо отметить, что, несмотря на внешнюю простоту процедуры вывода в силлогистике, в ней, как в капле воды, отражаются все те трудности, которые связаны с поиском вывода. Прежде всего это трудности понимания поступающих в систему сообщений, истолкования их в терминах, понятных на уровне внутреннего языка (в нашем случае это необходимость в процедурах нормализации сообщений). Затем это ряд трудностей, вызываемых процедурами проверки поступающего сообщения на согласованность содержащейся в нем информации с той информацией, которая ранее хранилась в памяти системы. Это трудности поиска, не опирающегося на какую-то цель, или при известной цели (в случае доказательства теоремы) не опирающегося на какие-либо соображения о путях движения по дереву вывода. Наконец, это трудности, связанные с прекращением процедур вывода и формированием отрицательного ответа на поставленный перед системой вопрос о выводимости.

Все эти трудности в той или иной форме будут присущи и другим системам моделирования человеческих рассуждений, ибо они являются принципиальными для всех формальных систем , частным случаем которых является силлогистика Аристотеля.

Формальная система – это четверка вида

Ф=< T , L , Q , R >.

Множество Т есть множество базовых элементов , исходных кирпичиков, не расчленяемых на более простые. Примерами таких элементов служат буквы (графемы) или детали в детском конструкторе. Единственное требование к элементам множества Т состоит в том, что для любого элемента за конечное число шагов можно узнать, принадлежит он Т или нет, а также отличить одни элементы от других, отождествляя одинаковые элементы.

Множество L есть множество синтаксических правил . С их помощью из элементов множества Т строятся более сложные образования, которые называются синтаксически правильными . Так, из графем возникают линейно упорядоченные сочетания, называемые словами, предложениями (для их образования используется специальный знак – пробел и знаки пунктуации), текстами; из деталей детского конструктора возникают более сложные образования, в которых отдельные элементы набора соединяются крепежными элементами.

Множество Q состоит из выделенных на основе некоторого соображения синтаксически правильных образований. Такое множество называется начальным или априорно принимаемым. Часто синтаксически правильные образования, входящие в Q , называют аксиомами . Тогда Q называют множеством аксиом .

Наконец, R представляет собой совокупность процедур, с помощью которых можно получать одни синтаксически правильные совокупности из других. Эти процедуры носят название правил вывода .

Формальные системы обладают одним общим свойством – автономностью. Если в такой системе задать все четыре множества, то она самостоятельно начнет генерировать множество выводимых в ней синтаксически правильных совокупностей. Они будут порождаться в результате применения различными способами правил вывода к совокупностям из множества Q . Сами элементы Q считаются в данной формальной системе выведенными всегда, т.е. априорно выведенными.

Легко усмотреть, что силлогистика Аристотеля и ее расширения, описанные нами, являют собой пример формальной системы. В качестве элементов Т выступают буквы, символизирующие имена конкретных сущностей и имена классов, а также символы А , Е , I и О . Синтаксические правила образуют из этих элементов нормальные формы представления высказываний Asp , Esp и т.п. В качестве исходных аксиом выступают законы силлогистики. 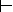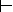Наконец, правилами вывода являются фиксированные выводы с одной посылкой, предназначенные для эквивалентных преобразований высказываний (например, Esp Eps ), а также таблица получения заключений в правильных модусах при наличии посылок для этих заключений. Такая силлогистическая система способна при заданном множестве, в состав которого кроме законов силлогистики входит некоторое число высказываний, принятых в этой системе за априорно выведенные, породить все высказывания, которые вытекают из Q и правил вывода для силлогизмов.