Владимир Сурдин - Разведка далеких планет

Рис. 4.3. Перемещение Урана на фоне звезд за двое суток. Наблюдение Патрика Мура 4 и 6 марта 1960 г.

Весть о новой планете, которую позже назвали Ураном, мгновенно облетела научный мир. Странно, но мысль о том, что в Солнечной системе может быть неизвестная планета, никогда прежде не приходила в голову астрономам. Они стали просматривать старые журналы наблюдений и обнаружили, что до 1781 г. новая планета уже была замечена не менее 20 раз! Впервые это произошло еще в 1690 г. Но каждый раз ее ошибочно принимали за звезду. Однако трудами Гершеля исторические предрассудки наконец были сломлены, и мысль о новых, не открытых пока планетах стала носиться в воздухе.

Аза несколько лет до этого произошло никем не замеченное событие – была обнаружена математическая закономерность в размерах планетных орбит. Впрочем, первые успешные опыты в этом деле принадлежат немецкому математику и астроному, мистику и астрологу Иоганну Кеплеру (1571–1630). Именно он, увлеченный «гармонией сфер», нашел соответствие между идеальными геометрическими фигурами и орбитами планет. Оказалось, что пять правильных многогранников, так называемых Платоновых тел – тетраэдр, куб, октаэдр, додекаэдр, икосаэдр – можно разместить внутри совокупности концентрических сфер, радиусы которых соотносятся так же, как радиусы планетных орбит (рис. 4.4). Кеплер опубликовал свою находку в знаменитой книге «Космографическая тайна» (1596 г.) и там же отметил, что между орбитами Марса и Юпитера существует слишком уж большой промежуток, в котором без труда уместилась бы орбита еще одной планеты.

Нельзя сказать, что геометрическая находка Кеплера привлекла всеобщее внимание: человеку, не обладающему пространственным воображением в той же мере, что и Кеплер, трудно было уловить найденную им тонкую геометрическую связь и тем более восхититься ею. К тому же в геометрических построениях Кеплера все правильные многогранники были исчерпаны, поэтому его «теория» не давала прогноза для положения неизвестных планет. Да и сам Кеплер вскоре доказал, что орбиты планет – не окружности, а эллипсы, так что простые геометрические аналогии с многогранниками оказались совершенно неуместны. И все же разрыв между орбитами Марса и Юпитера был так велик, что время от времени среди астрономов раздавались призывы поискать там планету.

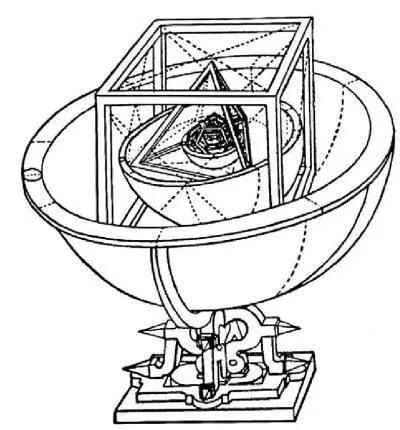
Рис. 4.4. Рисунок из книги Кеплера «Космографическая тайна», показывающий размещение 5 правильных многогранников внутри совокупности концентрических сфер.

Спустя полтора столетия после работы Кеплера была сделана значительно более простая и убедительная математическая находка, подтвердившая существование «гармонии сфер» и позволившая прогнозировать орбиты неизвестных планет. В 1766 г. немецкий математик Иоганн Даниель Тициус фон Виттенберг (1729–1797) опубликовал свой перевод книги известного естествоиспытателя Шарля Боне «Созерцание природы». Но Тициус не ограничился переводом текста, а сделал к нему небольшое примечание, причем в очень необычной и скромной форме: он попросту внес свое добавление в основной текст. Смысл этого примечания состоял в следующем: расстояния планет от Солнца подчиняются простому эмпирическому правилу, а точнее говоря – простой числовой последовательности. Если принять расстояние Земли от Солнца за 10 условных единиц, то расстояния остальных планет составят R n= 4 + 3 · 2 n, где n = – ∞ для Меркурия и п = 0,1, 2…. для последующих планет. Табл. 4.1. иллюстрирует это правило. Все расстояния даны в ней в астрономических единицах (а. е.), равных расстоянию Земли от Солнца. Плутон и астероиды вставлены для полноты картины. Оценивая точность формулы Тициуса, нужно иметь в виду, что в то время ни один из астероидов, а также Уран, Нептун и Плутон еще не были открыты.

Таблица 4.1

К правилу Тициуса – Боде

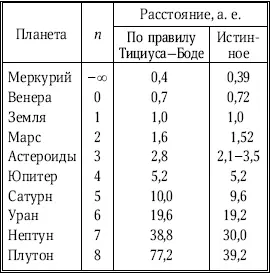
Таблица показывает, что простая формула Тициуса очень хорошо описывает размеры орбит известных в те годы планет. Но этот замечательный факт вызвал интерес лишь у нескольких специалистов. Имя Тициуса не стало известным.