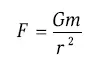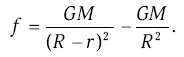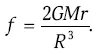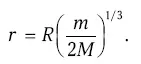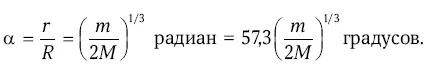Владимир Сурдин - Разведка далеких планет

Неудивительно, что неспециалисту многочисленные спутники планет кажутся «все на одно лицо». Лишь упоминание Луны вызывает у несведущего человека интерес и некоторые ассоциации. А со спутниками других планет не связаны легенды и предания, в их честь не совершали жертвоприношения, древние народы не использовали их для счета времени. Однако для специалиста-планетолога каждый спутник – это уникальный мир, не менее важный и интересный, чем наша вечная соседка Луна. Более того, система спутников каждой планеты – это своеобразный аналог Солнечной системы, со своими закономерностями в распределении спутников по орбитам и их физическим свойствам. Поэтому поиск новых спутников будет продолжаться как вглубь – ко все более мелким телам, так и вширь – охватывая все большую область вокруг каждой планеты. В связи с этим зададимся вопросом: каков максимально возможный размер спутниковой системы?

Поскольку спутником мы называем объект, постоянно сопровождающий планету, то максимальный размер системы спутников определяется областью гравитационного контроля планеты. Хотя она и не совсем сферическая, ее принято называть сферой Хилла. Если отвлечься от деталей, то на границе этой области, очевидно, должно наступать равенство двух сил: силы притяжения спутника к планете ( F ) и силы, действующей со стороны Солнца и старающейся «оторвать» спутник от планеты ( f ). Силу f обычно называют приливной, поскольку именно она, действующая со стороны Луны и Солнца, вызывает приливы в океанах и теле Земли. Найдем эти силы в расчете на единицу массы спутника. Пусть M и m — массы Солнца и планеты, R и r – расстояние планеты от Солнца и спутника от планеты, G – постоянная тяготения. Тогда

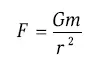
и

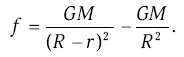
Полагая, что R ≫ r , мы легко преобразуем выражение для f (отбросив малые величины) к виду

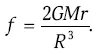
Тогда радиус сферы Хилла ( r ) определится равенством F=f и составит

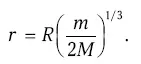
Эта формула не учитывает характера движения спутников, но для оценок она годится. Поскольку нас в основном интересуют системы спутников планет-гигантов (R ≫ 1 а. е.), то угловой радиус их сфер Хилла для земного наблюдателя составит

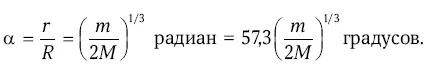
Например, для Юпитера (М/т ≈1000) получим α = 4,5°. А в противостоянии, когда Земля и Юпитер сближаются на минимальное расстояние и поиск спутников наиболее продуктивен, это значение возрастает до 5,6°. Следовательно, астроному приходится вести поиск в круге диаметром 11,2°, что по площади равно 500 лунным дискам! Для Сатурна диаметр зоны спутников составляет 6°, для Урана и Нептуна – около 3°. Именно таковы наблюдаемые с Земли предельные размеры спутниковых систем планет-гигантов.

А насколько исчерпаны эти области? Насколько близки к их границам наиболее далекие известные спутники планет? Самый удаленный спутник Юпитера (S/2003 J2) в противостоянии планеты отходит от нее для земного наблюдателя на 3,3°. То есть до границы остается еще 2,3° – изрядная область для поиска неизвестных объектов. В системе спутников Сатурна самый далекий (Бестла) виден на расстоянии 1,6° от планеты: до границы еще 1,4°. Внешний спутник Урана (Фердинанд) удаляется на 0,6°, а внешний спутник Нептуна (Несо) – на 1°. Как видим, у всех этих планет осталось большое пространство в сфере Хилла, где могут прятаться неизвестные спутники. Разумеется, вблизи границ этих областей движение спутников неустойчиво и связь с планетой очень слаба. Уже найденные там объекты движутся хаотически, но все же они могут жить там довольно долго. Возможно, эти спутники иногда теряют связь с планетой, а затем они – или им подобные – возвращаются в ее гравитационные объятия. Там их и надо искать.

Кстати, на периферии сферы Хилла могут прятаться не только отдельные спутники, но даже кольца планет! Так, в мае 2009 г. удалось обнаружить ранее неизвестное кольцо Сатурна, самое большое среди планетных колец: для земного наблюдателя его угловой размер составляет около 1°, вдвое больше лунного диска! К сожалению, наблюдать этот колоссальный объект в оптическом диапазоне невозможно из-за его крайней разреженности. Глазом его не увидеть, даже находясь непосредственно в нем. Как же оно было открыто? Новое кольцо в основном состоит из частиц пыли и льда, температура которых около 80 К. Именно из-за такой сравнительно высокой температуры его заметил космический телескоп «Спитцер», наблюдающий в дальнем инфракрасном диапазоне (см. с. 15 цветной вкладки).