Пекка Теерикор - Эволюция Вселенной и происхождение жизни

В «Изложении системы мира» содержатся и пророческие слова о том, что «гравитация небесного тела может быть настолько сильна, что свет не сможет его покинуть». Такие тела сейчас называют черными дырами. Эту же идею еще раньше, в 1784 году’, высказал Джон Мичелл. Оба ученых пришли к ней независимо друг от друга (см. главу 15).

Вычисление возмущенной орбиты Луны — трудная задача; говорят, что она единственная вызывала затруднения даже у сэра Исаака. Частично это связано с тем, что нужно учитывать притяжение Луны не только Землей, но и Солнцем. Вслед за Ньютоном этой проблемой занялись великие практики небесной механики — французский математик Жан Лерон Д’Аламбер (1717–1783) и швейцарский астроном Леонард Эйлер (1707–1783), проработавший большую часть жизни в Санкт-Петербурге. Оба они пытались объяснить сложное движение Луны и связанные с ним изменения ориентации оси вращения Земли. Прецессия земной оси происходит с периодом 26 000 лет, и к тому же ось совершает небольшие колебания с периодом 18 лет, связанные с периодом затмений, саросом, упомянутым в главе 1. Эти колебания — их называют нутацией — были открыты Джеймсом Брадлеем в 1748 году. А через год Д’Аламбер опубликовал теорию нутации, основанную на Ньютоновой механике. Он сообщил результаты своей работы Эйлеру, который счел эту теорию трудной для чтения. Эйлер создал упрощенную версию теории Д'Аламбера, но по неизвестной причине не упомянул в этой работе имя самого Д’Аламбера. Это привело к разрыву отношений между двумя выдающимися учеными своего времени. Позже Эйлер извинился, но это не спасло положения.

Еще одной сложной задачей оказалось явление приливного трения. Приливы служат причиной постепенного замедления вращения Земли. Вызывая приливы, Луна пытается затормозить вращение Земли до своего собственного орбитального периода, но это, в свою очередь, удлиняет орбитальный период Луны. В конце концов земные сутки и лунный месяц станут одинаковыми — 55 современных суток каждый. При этом Луна окажется гораздо дальше от Земли, чем сейчас. Но эти изменения происходят очень медленно. За прошедшие 400 млн лет наши сутки удлинились с 22 до 24 часов. Изменения подтверждаются слоистой структурой ископаемых раковин и кораллов, которую используют для подсчета количества дней и месяцев в году в период их жизни, так же как определяют возраст дерева по количеству колец на спиле его ствола. Кораллы за сутки наращивают один очень тонкий слой извести. Можно посчитать эти суточные линии роста. Их толщина меняется в течение года. Так что, имея хороший кусок коралла, можно вычислить, сколько суток было в году в ту эпоху (рис. 11.2).

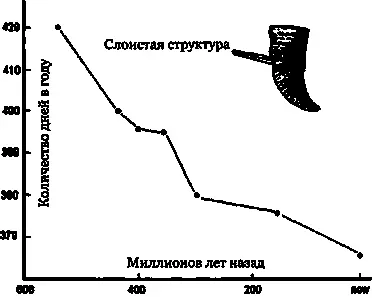
Рис. 11.2. За последние 600 млн лет количество дней в году уменьшилось примерно от 420 до 365 суток. На это указывает подсчет слоев в окаменелых ракушках и кораллах. Таким образом, в прошлом сутки были короче, чем сейчас.

Наряду с долговременными эффектами приливного трения система Земля-Луна-Солнце демонстрирует нам пример относительно простой задачи трех тел с очень массивным Солнцем, расположенным очень далеко от двух других тел. Запуская космический корабль в сторону Луны, мы вынуждены решать гораздо более сложную задачу трех тел при сравнимых расстояниях между ними: в каком направлении и с какой скоростью мы должны запустить маломассивный космический корабль из окрестности Земли, чтобы он попал на Луну по удобной орбите. В общей задаче трех тел, имеющих сравнимые массы и движущихся на сравнимых расстояниях друг от друга, орбиты становятся еще сложнее (рис. 11.3).

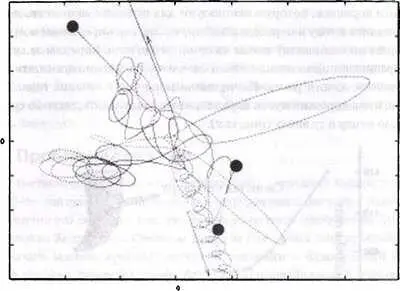
Рис. 11.3. Орбиты в системе трех тел. Эти орбиты сложно извиваются, пока одно из тел не оказывается выброшенным, а два других остаются рядом, образовав двойную звезду, компоненты которой обращаются один вокруг другого. Это результат компьютерного моделирования, проведенного Сеппо Миккола в обсерватории Туорла (Университет г. Турку).

Время от времени два тела тесно сближаются, в то время как третье тело держится на расстоянии. Сближения повторяются вновь и вновь, причем члены тесной пары меняются. И это продолжается вплоть до распада системы, когда одно из трех тел окончательно выбрасывается. После этого орбиты становятся простыми: остается двойная система с эллиптическими орбитами, а третье тело удаляется от этой двойной. Формы и размеры окончательных орбит можно посчитать статистическим методом, но что произойдет в каждом конкретном случае, удается определить только путем долгих и точных вычислений. Часто нам вполне достаточно статистического описания. Например, в звездном скоплении сближения трех тел случаются часто, поэтому интерес представляет только их статистический эффект.