Пекка Теерикор - Эволюция Вселенной и происхождение жизни

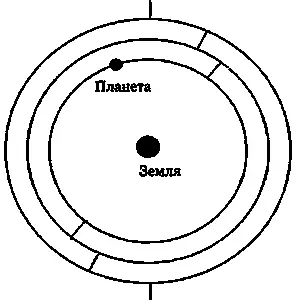
Рис. 3.2. Упрощенная диаграмма концентрических сфер Евдокса. Сферы вращаются вокруг своих осей с различными, но постоянными скоростями. Оси соединяют каждую внутреннюю сферу со следующей, внешней, и они наклонены друг к другу на определенные углы. Поэтому траектория планеты, видимая с Земли, не круговая, а более сложная.

Первая сфера вращается вокруг оси север-юг и дает суточное движение. Один полный поворот второй сферы, наклоненной к первой на угол наклона эклиптики к небесному экватору, обеспечивает сидерический период. Наконец, третья сфера моделирует вращение по орбите, наклоненной к эклиптике. В случае Луны и Солнца достаточно трех сфер (Евдокс ошибочно считал, что Солнце движется не точно по эклиптике). Планеты с обратными петлями — Меркурий, Венера, Марс, Юпитер и Сатурн — для объяснения их более сложного движения требуют наличия четырех сфер у каждой. Таким образом, полное количество сфер составляет (2 х 3) + (5 х 4) = 26, и все они концентрически вложены друг в друга.

С помощью своей модели Евдокс мог неплохо объяснить движения планет, известные в то время. Однако Марс оказался крепким орешком, и его движение было почти невозможно описать с помощью этой модели. Видимо, Евдокс рассматривал свою модель не как реальную физическую конструкцию, а как чисто математическое построение, где ряд сфер одной планеты никак не влияет на сферы другой, хотя все они вложены одна в другую.

Развитием модели Евдокса стала планетная модель Аристотеля, включавшая 56 сфер с Землею в центре. Возможно, Аристотель рассматривал сферы как физические объекты, типа небесного кристалла. Однако он отвергал идею Пифагора о музыке сфер. Наоборот, он рассматривал тишину небес как доказательство наличия сфер. Шума можно было бы ожидать, если бы небесные тела неслись сквозь какую-то среду. Число сфер возросло, поскольку Аристотель хотел соединить ряд сфер каждой планеты с дополнительными сферами, так чтобы основное суточное движение внешней сферы неподвижных звезд передавалось сверху вниз.

Планетная модель Евдокса не смогла объяснить некоторые наблюдательные данные, и это обнаружил Автолик из Питаны (около 360–290 до н. э.). Когда планеты делают петлю на западе, они ярче, чем в остальное время, что означает, что в этот момент они к нам ближе. В моделях, где центр сфер расположен на Земле, планеты всегда остаются на одном и том же расстоянии от Земли. Это несоответствие было устранено Аполлонием Пергским (около 265–176 до н. э.). Он работал в новом мировом научном центре — в Александрийском музее. Аполлоний был учеником Евклида и был известен своими исследованиями геометрических кривых — эллипса, гиперболы и параболы. Гораздо позже эти кривые сыграли важную роль в изучении планетных орбит. Аполлоний разработал новый, хотя и основанный на тех же идеальных окружностях, способ представления планетных движений.

В его модели планета не укреплена на своей сфере, а движется по маленькой окружности — эпициклу, центр которого закреплен на равномерно вращающейся главной сфере. Когда планета перемещается в обратном направлении по эпициклу, она находится в наиболее близком к нам положении, и этим объясняется ее поярчание при совершении обратной петли на небе (рис. 3.3). Движение по большому кругу — дифференту происходит с сидерическим периодом планеты, в то время как по эпициклу она вращается с синодическим периодом. Вращение в обоих случаях происходит с постоянной скоростью. Эпицикл объяснял изменение блеска каждой планеты и ее движение по небу, заменяя две сферы для обратного движения. Эта схема использовалась и совершенствовалась до конца Средневековья.

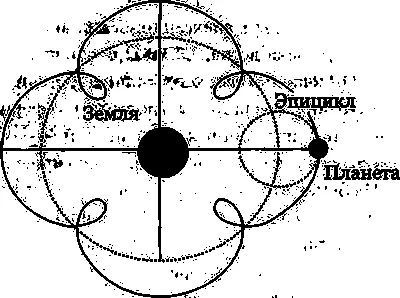
Рис. 3.3. Схематическое изображение модели эпициклов. Планета движется по малому кругу (эпициклу), центр которого движется по большому кругу (деференту), а в центре его расположена Земля.

Мы практически ничего не знаем о жизни Гиппарха (около 190–120 до н. э.), и его труды почти полностью утеряны, но все же нет никаких сомнений, что это был великий астроном, живший на острове Родос и в других местах. Он разработал тригонометрию, необходимую для астрономии, где в вычислениях используются треугольники. Кроме того, он создал каталог звезд, включающий более 8оо светил, описание их положения на небе и их яркости, выраженной в звездных величинах, единицах, используемых до сих пор. Самым ярким звездам Гиппарх приписал первую величину. Для звезд, с трудом различимых на небе невооруженным глазом, была указана шестая звездная величина, а для остальных звезд диапазон звездных величин составил от 2 до 5.