Пекка Теерикор - Эволюция Вселенной и происхождение жизни

Рис. 2.3. Фреска Рафаэля, изображающая философа Платона со своим самым знаменитым учеником Аристотелем во время дискуссии в Афинской Академии. Платон указывает пальцем вверх, на небо, а подход Аристотеля более приземлен. Гипатия (жившая несколькими веками позже), одетая в белое платье, стоит внизу слева, одна, повернувшись к зрителям, в окружении мужчин.

Вавилонские наблюдатели неба знали о блуждающих небесных объектах (планетах; в то время это понятие было более широким, чем сейчас). Один из них, Солнце, всегда движется на фоне звезд по эклиптике к востоку. Это его годичный путь по зодиакальным созвездиям. Луна, не удаляясь значительно от эклиптики, делает один оборот по звездному небу примерно за месяц. Остальные планеты гоже большую часть времени медленно перемещаются к востоку, оставаясь недалеко от эклиптики. Требуется определенное время, чтобы планета сделала полный оборот от некоторого созвездия в зодиаке к тому же самому месту (ее сидерический период). Но, в отличие от Солнца и Луны, прочие планеты иногда замедляют движение, останавливаются и некоторое время движутся в обратном направлении, а затем вновь останавливаются и возвращаются к своему нормальному движению (рис. 3.1).

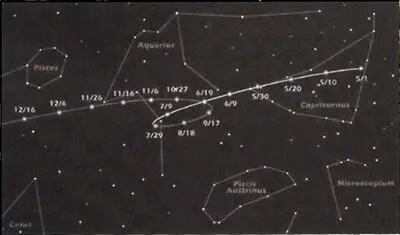
Рис. 3.1. Обратное движение Марса в 2003 году. Его синодический период в 780 суток отделяет одну петлю от другой, которые располагаются в разных эклиптикалъных созвездиях. Это было основньш явлением, которое древние ученые и позже (более успешно) Коперник пытались объяснить с помощью моделей движения. Рисунок: NASA/JPL–Caltech.

Существует определенная регулярность в этом необычном попятном движении. У каждой планеты свой синодический период — промежуток времени между двумя последовательными попятными петлями. Синодический период отличается от сидерического, и поэтому каждая следующая остановка происходит в ином созвездии зодиака. В табл. 3.1 приведены синодические и сидерические периоды планет (из которых Уран, Нептун и Плутон не были известны в древности).

Таблица 3.1. Синодический и сидерический периоды планет (включая планеты, открытые в недавнее время).

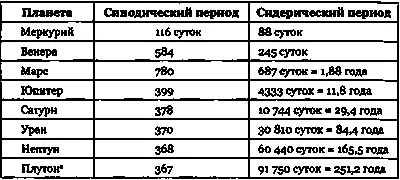
* Согласно современному определению, Плутон не являе т ся большой планетой: это карликовая планета. Обратите внимание, что с увеличением сидерического периода синодический период становится все ближе к нашему году (можете объяснить, почему?).

Греческие философы начали использовать новый подход, выходящий за рамки астрологии: они пытались рационально объяснить видимое движение планет. Их идеалом небесных движений были сферы и круговые движения (и этот идеал продержался два тысячелетия). Сфера и окружность как геометрические фигуры были хорошо изучены греческими математиками. Кроме того, при идеальном круговом движении точка всегда возвращается в исходное положение, а это, очевидно, подходит для небесных объектов, которые если и не божественные существа, то, по крайней мере, вечные; а небесная сфера, судя по наблюдениям, вращается совершенно равномерно.

Платон спрашивал своих учеников, какого типа простое движение может объяснить сложные движения планет. Евдокс (около 408–355 до н. э.) принял вызов. Среди прочих достижений Евдокса был метод вывода формулы для вычисления площадей и объемов, похожий на современное интегральное исчисление.

Теория Евдокса о сферах, концентрических по отношению к Земле, стала первой математической моделью, объясняющей некоторые детали небесных движений, включая и сбивающие с толку попятные движения. В этой модели рассматривались сферы, вращающиеся вокруг своей оси с различными, но постоянными скоростями. Ось каждой внутренней сферы упиралась в следующую сферу, и все они были наклонены друг к другу под определенным углом. За пределом всех планетных сфер располагалась небесная сфера неподвижных звезд, вращающаяся равномерно вокруг Земли с периодом в одни сутки. Мы надеемся, что наше краткое объяснение не ошеломило читателя! Ряд взаимосвязанных сфер обеспечивал каждой планете ее собственное особое движение. Довольно равномерное движение Солнца и Луны можно смоделировать всего лишь тремя сферами для каждого из объектов. Основная идея этой теории схематически представлена на рис. 3.2.