Шинтан Яу - Теория струн и скрытые измерения Вселенной

В области исследований минимальных поверхностей присутствует некоторая путаница, берущая свое начало в терминологии, не изменявшейся на протяжении столетий, несмотря на постепенное усложнение математических понятий. Дело в том, что существует еще один класс поверхностей, которые также иногда называют минимальными, хотя они и не обязательно имеют минимальную площадь. Этот класс включает поверхности, площадь которых меньше, чем площадь других поверхностей, ограниченных тем же контуром, — это могут быть как истинно минимальные поверхности или «основные состояния» так и поверхности, носящие название стационарных, которые имеют минимальную возможную площадь на отдельных участках (локально), но не в целом (глобально). Поверхности этого типа, имеющие нулевую нормальную составляющую поверхностного натяжения и нулевую среднюю кривизну, весьма интересны как математикам, так и инженерам. Мы привыкли думать о минимальных поверхностях как о членах одного семейства, весьма похожих между собой. И поскольку каждая из этих поверхностей по-своему интересна, все их можно считать уникальными.

Нахождение кратчайшего пути является одномерным вариантом более сложной задачи нахождения минимальной поверхности для большего числа измерений. Кратчайший путь между двумя точками — будь то прямая линия, плоскость или дуга окружности, соединяющая две точки на земном шаре, — иногда называют геодезической линией , хотя это понятие, также вызывая путаницу, включает в себя и те пути, которые не обязательно являются кратчайшими, что, впрочем, не мешает им иметь большое значение для геометров и физиков. Если на дуге большого круга взять две точки, не лежащие на противоположных полюсах, то возникнет сразу два возможных пути из одной точки в другую — короткий и длинный. Оба пути представляют собой геодезические линии, но лишь один из них соответствует кратчайшему расстоянию между точками. Более длинный путь также имеет минимально возможную длину, однако только локально, среди всех возможных путей, проходящих вблизи данной геодезической линии. При рассмотрении всех возможных вариантов этот путь уже не будет кратчайшим — более кратким будет противоположный ему путь. Ситуация становится еще более запутанной в случае эллипсоида — поверхности, имеющей форму сплюснутой сферы, которую можно получить, вращая эллипс вокруг одной из его осей, — на эллипсоиде существует много геодезических линий, не являющихся кратчайшими путями из всех возможных.

Для нахождения упомянутых выше минимальных путей необходимо использовать дифференциальные уравнения. Чтобы найти минимальные значения, необходимо обратить внимание на точки, в которых производная равна нулю. Поверхность с наименьшей площадью должна удовлетворять определенному дифференциальному уравнению, а именно такому уравнению, которое выражает факт равенства нулю средней кривизны во всех возможных точках поверхности. Как только вы нашли требуемое дифференциальное уравнение в частных производных — вы сразу же получаете огромное количество информации о вашей задаче, поскольку за годы работы мы узнали многое об этих уравнениях.

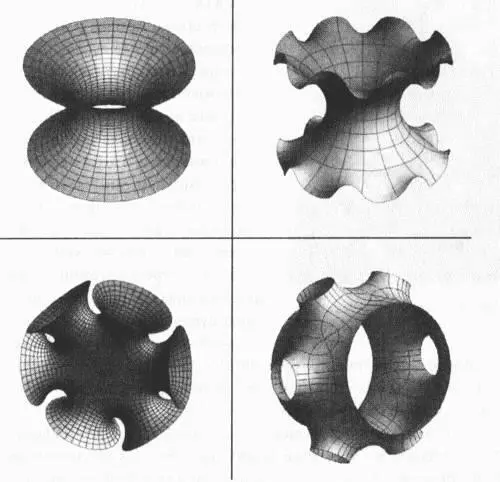
Рис. 3.6.Хотя оригинальная формулировка проблемы Плато относится к поверхностям, натянутым на простые замкнутые кривые, можно сформулировать более сложные варианты того же вопроса — и иногда даже найти на них ответы. Например, можно ли найти минимальную поверхность в том случае, если граница состоит не из одной, а из нескольких замкнутых кривых (например, окружностей)? На рисунке приведены некоторые примеры минимальных поверхностей, являющихся решениями проблемы Плато, представленной в данной форме. (Исходное изображение — 3D-XplorMath Consortium)

«Впрочем, это совсем не означает, что мы занимаемся разграблением хорошо разработанной области и просто подбираем все, что плохо лежит. Наше сотрудничество — это скорее улица с двухсторонним движением, поскольку большой объем информации о поведении дифференциальных уравнений в частных производных был получен именно благодаря геометрии», — говорит Роберт Грин. [28] Greene, interview with author, March 13, 2008. Чтобы увидеть то, что может получиться из соединения геометрического анализа с теорией минимальных поверхностей, давайте продолжим наш разговор о мыльных пленках.

В XIX столетии бельгийский физик Жозеф Плато провел в этой области серию классических экспериментов, состоявших в погружении изогнутых различными способами кусков проволоки в сосуды с мыльной водой. Плато сделал вывод, что мыльные пленки, которые образовывались в ходе эксперимента, всегда имели минимальную поверхность. Более того, он предположил, что для любой замкнутой кривой всегда можно найти минимальную поверхность, контуром которой служила бы данная кривая. В большинстве случаях будет существовать только одна минимальная поверхность — и тогда задача будет иметь единственное решение. Но в некоторых случаях существует больше чем одна поверхность с минимальной площадью, и мы не знаем, сколько их будет всего.