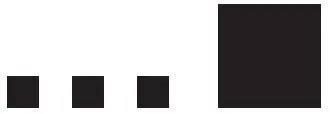Ольга Шиян - Развитие творческого мышления. Работаем по сказке

После этого уже не составит труда подобрать квадрат для медведя, но после этого стоит задать провокационный вопрос, чтобы понять, насколько сознательно дети дали ответ:

— А может, стоит для медведя выбрать квадрат побольше? Медведь вон какой большой.

Если дети поддаются на провокацию, надо обсудить этот вопрос, пока они не придут к выводу, что при сравнении по хитрости именно лиса должна обозначаться самым большим квадратом.

После этого обсуждается и значок для лисы: скорее всего дети сами предложат выбрать большой квадрат, а если нет — надо вспомнить, что лиса оказалась самой хитрой, а они как раз выстраивают героев по хитрости.

В итоге на доске должны получиться две серии:

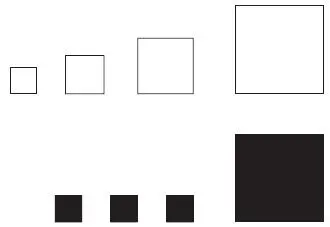
В конце занятия педагог указывает на две получившиеся модели (они располагаются друг под другом) и удивляется:

— Как же так получилось, что у нас два ряда героев?

Дети указывают, что в одном ряду герои построены «по росту», а в другом — по хитрости. Если задание оказывается трудным для ребят, надо поиграть в «Угадайку»: предложить им по квадратам угадать героев и основание для сравнения.

После этого остается с теми детьми, которые не были активны на занятии, уточнить еще раз, что означает каждая модель, и предложить загадать эту загадку родителям.

4. Решаем диалектическую задачу с помощью наглядной модели

Цель.Решение диалектической задачи с помощью наглядной модели.

Материалы.Картинки с изображением персонажей, черные квадраты (8×8, 11×11, 14×14, 17×17 см — по три квадрата каждого размера).

В решении предыдущих задач фигурировали только те персонажи, с которыми встречался колобок, а вот о самом колобке вопрос не ставился. На этот раз детям предлагается решить диалектическую задачу: оценить хитрость колобка.

Дети могут попасть в «формально-логическую ловушку»: обнаружить только одну из характеристик колобка (хитрый — потому что от зайца, волка, медведя ушел; нехитрый — потому что от лисы не ушел), забыв о печальном финале сказки.

В начале занятия можно предложить детям изобразить квадратиками героев сказки по размеру и по хитрости. Все возникающие ошибки стоит обсуждать, предлагая детям обосновывать свою точку зрения. Главная задача на этом этапе «повторения» — делать акцент на разных основаниях для сравнения и на том, что в зависимости от основания серии выстраиваются по-разному.

Воспитатель помещает в центр доски серию «по хитрости» и задает проблемный вопрос: «А вот если бы вы сюда и колобка поместили, то каким бы квадратиком его обозначили?»

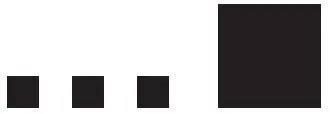
Если дети говорят, что таким же квадратом, как лису, надо выполнить это указание и «прочитать» модель так:

— Итак, у нас получилось, что заяц, волк и медведь — бесхитростные, а колобок и лиса хитрые, отличаются от всех.

Обоснование противоположных суждений.

Тут наверняка кто-то возразит, что не так уж хитер колобок — его-то лиса перехитрила.

— Тогда давайте обозначим его маленьким квадратом. А теперь что получилось? Что все звери и колобок бесхитростные, а одна лиса хитрая.

Если никто не возразит, надо задать контрвопрос:

— А разве звери смогли колобка перехитрить? Как он от них ушел? Может, стоит его большим квадратом обозначить?

Дети должны вспомнить, что колобок все же действовал разумно — песенку пел, внимание отвлекал и от всех, кроме лисы, укатился.

— Так как же нам обозначить колобка, каким квадратом?

Диалектическое преобразование.

«Хорошим» ответом тут будет предложение обозначить колобка средним квадратом и обоснование, что он обманул некоторых зверей, но его самого перехитрила лиса, т. е. он хитрее волка с зайцем и медведем, а лиса хитрее его.

5. Разыгрываем сказку с помощью наглядной модели

Цель.В символической форме отразить содержание сказки.

Материалы.Две наглядные модели сказки «Колобок», отражающие смену альтернативы в сказке; карточки-значки с изображением персонажей сказки — колобка, зайца, волка, медведя и лисы (все карточки-значки должны быть одинакового размера).

Перед началом занятия на доске располагается картинка с «Колобком» и обе наглядные модели сказки. Сначала надо предложить детям вспомнить, как «читаются» сказки по наглядной модели, спросить, кто может «расшифровать» сказку, «прочитать» ее по квадратикам. Можно задать вопросы о том, почему белые квадратики на одной модели увеличиваются, а на другой три квадратика не различаются по размеру.