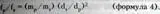Айзек Азимов - О времени, пространстве и других вещах. От египетских календарей до квантовой физики

Нам интересно узнать, насколько гравитационная сила, действующая между спутником и планетой, сравнима с аналогичной силой, действующей между спутником и Солнцем. Иными словами, чрезвычайно любопытно вычислить отношение f р/f s. которое можно назвать «коэффициентом перетягивания каната». Чтобы его получить, следует разделить формулу 2 на формулу 3. Результат приведен в формуле 4:

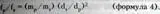
При делении формула несколько упростилась. Во-первых, исчезла гравитационная постоянная, и нам не придется иметь дело с малыми числами и неудобными размерностями. С другой стороны, сократилась масса спутника (иными словами, для получения «коэффициента перетянутого каната» не имеет значения размер спутника).

В формуле остались отношение массы планеты к массе Солнца, а также квадрат отношения расстояния от спутника до Солнца к расстоянию от спутника до планеты.

Спутники имеют только шесть планет. Это Нептун, Уран, Сатурн, Юпитер, Марс и Земля (в порядке убывания расстояния от Солнца).

Произведя подсчет отношения масс, получим следующие результаты:

Как видите, отношение масс явно в пользу Солнца. Даже Юпитер — самая тяжелая из планет — не дотянул до 1/ 1000массы Солнца. В действительности суммарная масса всех планет (с учетом спутников, астероидов, комет и метеоритов) составляет не более 1/ 750массы Солнца.

Пока у Солнца имеются все шансы выиграть соревнования по перетягиванию каната.

Однако нам следует рассмотреть и отношение расстояний, а здесь все говорит в пользу планеты, потому что любой спутник располагается ближе к своей родной планете, чем к Солнцу. Тем более, что это отношение расстояний следует еще возвести в квадрат. После этого уже можно почти не сомневаться, что Солнце не перетянет канат. Но все-таки проверим.

Начнем с Нептуна. Он имеет два спутника — Тритон и Нереиду. Среднее расстояние каждого из них от Солнца примерно такое же, как среднее расстояние Нептуна от Солнца, — 2 797 000 000 миль. Среднее расстояние Тритона от Нептуна — 220 000 миль, а среднее расстояние Нереиды от Нептуна — 3 460 000 миль.

Разделив расстояние от Солнца на расстояние от Нептуна до каждого спутника и возведя результат в квадрат, получим 162 000 000 для Тритона и 655 000 для Нереиды. Умножив каждое из этих чисел на отношение масс Нептуна и Солнца, получим следующие коэффициенты:

Тритон 8400

Нереида 34

Таким образом, условия, в которых существуют спутники, очень различны. Гравитационное влияние Нептуна на свой ближайший спутник Тритон — намного больше, чем влияние па него Солнца. Нептун схватил Тритон весьма уверенно. Притяжение Нептуном своего внешнего спутника — Нереиды — является значительным, но не подавляющим по сравнению с Солнцем. К тому же Нереида имеет эксцентричную орбиту, и более эксцентричной орбиты нет ни у одного спутника в Солнечной системе. 13 одном ее конце Нереида приближается к Нептуну на 800 000 миль, в другом удаляется более чем на 6 000 000 миль. 13 точке наибольшего удаления от планеты «коэффициент перетягиваемого каната» имеет необыкновенно низкую величину — всего лишь 11!

По многим причинам (одной из которых является эксцентричность ее орбиты) астрономы обычно считают, что Нереида является не настоящим спутником Нептуна, а малой планетой, случайно попавшей в его гравитационное поле.

То, что Нептун так слабо держит Нереиду, казалось бы, подтверждает это. Действительно, объединение Нептуна и Нереиды вполне может быть временным явлением. Возможно, что эффект солнечного тяготения когда-нибудь вырвет спутник из объятий Нептуна. Зато Тритон никогда не покинет своего отца, конечно, если не произойдет катастрофы вселенского масштаба.

Я не стану приводить в этой книге подробные вычисления для всех спутников Солнечной системы. Поверьте, что я их выполнил, и теперь кратко познакомлю вас с основными результатами. Уран, например, имеет пять спутников, все они вращаются в плоскости экватора планеты, и астрономы не сомневаются, что все пять — настоящие спутники. Это Миранда, Ариель, Умбриель, Титания и Оберон.

«Коэффициенты перетягиваемого каната» для этих спутников следующие: