Christopher alexander - A pattern language

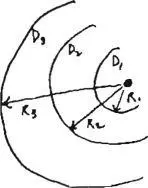A density gradient.

Imagine that the three rings of some actual neighborhood have densities Dj, D2, D3. And assume, now, that a new person moves into this neighborhood. As we have said, within the given density gradient, he will choose to live in that ring, where his liking for green and quiet just balances his liking for access to shops and public services. This means that each person is essentially faced with a choice among three alternative density-distance combinations:

Ring 1. The density Di, with a distance of about Ri to shops.

Ring 2. The density D2, with a distance of about Ro to shops.

Ring 3. The density D3, with a distance of about R3 to shops.

Now, of course, each person will make a different choice—ac

cording to his own personal preference for the balance of density and distance. Let us imagine, just for the sake of argument, that all the people in the neighborhood are asked to make this choice (forgetting, for a moment, which houses are available). Some will

choose ring I, some ring 2, and some ring 3. Suppose that Ni choose ring 1, N2 choose ring 2, and N3 choose ring 3. Since the three rings have specific, well-defined areas, the numbers of people who have chosen the three areas, can be turned into hypothetical densities. In other words, if we (in imagination) distribute the people among the three rings according to their choices, we can work out the hypothetical densities which would occur in the three rings as a result.

Nozv zve are suddenly jaced with two fascinating possibilities:

I. These new densities are different from the actual densities.

II. These new densities are the same as the actual densities.

Case I is much more likely to occur. But this is unstable—since

people’s choices will tend to change the densities. Case II, which is less likely to occur, is stable—since it means that people, choosing freely, will together re-create the very same pattern of density within which they have made these choices. This distinction is fundamental.

If we assume that a given neighborhood, with a given total area, must accommodate a certain number of people (given by the average density of people at that point in the region), then there is just one configuration of densities which is stable in this sense. We now describe a computational procedure which can be used to obtain this stable density configuration.

Before we explain the computational procedure , zve must explain how very fundamental and important this kind of stable density configuration is.

In today’s world, where density gradients are usually not stable, in our sense, most people are forced to live under conditions where the balance of quiet and activity does not correspond to their wishes or their needs, because the total number of available houses and apartments at different distances is inappropriate. What happens, then, is that the rich, who can afford to pay for what they want, are able to find houses and apartments with the balance that they want; the not so rich and poor are forced to take the leavings. All this is made legitimate by the middle-class economics of “ground rent”—the idea that land at different distances from centers of activity, commands different prices, because more or less people want to be at those distances. But actually the fact of differential ground rent is an economic

mechanism which springs up, within an unstable density configuration, to compensate for its instability.

We want to point out that in a neighborhood with a stable density configuration (stable in our sense of the word), the land would not need to cost different prices at different distances, because the total available number of houses in each ring would exactly correspond to the number of people who wanted to live at those distances. With demand equal to supply in every ring, the ground rents, or the price of land, could be the same in every ring, and everyone, rich and poor, could be certain of having the balance they require.

We now come to the problem of computing the stable densities for a given neighborhood. The stability depends on very subtle psychological forces; so far as we know these forces cannot be represented in any psychologically accurate way by mathematical equations, and it is therefore, at least for the moment, impossible to give a mathematical model for the stable density. Instead, we have chosen to use the fact that each person can make choices about his required balance of activity and quiet, and to use people’s choices, within a simple game, as the source of the computation. In short, we have constructed a game, which allows one to obtain the stable density configuration within a few minutes. This game essentially simulates the behavior of the real system, and is, we believe, far more reliable than any mathematical computation.

DENSITY GRADIENTS GAME

x. First draw a map of the three concentric half rings. Make ita half-circle—if you accept the arguments ofECCENTRIC nucleus (28)—otherwise a full circle Smooth this half-circle to fit the horseshoe of the highest density—mark its center as the center of that horseshoe.

2. If the overall radius of the half-circle is R, then the mean radii of the three rings are Ri,R 2,R 3given by:

Ra = 5 R/ 6

3. Make up a board for the game, which has the three concentric circles shown on it, with the radii marked in blocks, so people can understand them easily, i.e., 1000 feet = 3 blocks.

4. Decide on the total population of this neighborhood. This is

TOWNS

the same as settling on an overall average net density for the area. It will have to be roughly compatible with the overall pattern of density in the region. Let us say that the total population of the community is N families.

5. Find ten people who are roughly similar to the people in the community—vis-a-vis cultural habits, background, and so on. If possible, they should be ten of the people in the actual community itself.

6. Show the players a set of photographs of areas that show typical best examples of different population densities (in families per gross acre), and leave these photographs on display throughout the game so that people can use them when they make their choices.

7. Give each player a disk, which he can place on the board in one of the three rings.

8. Now, to start the game, decide what percentage of the total population is to be in each of the three rings. It doesn’t matter what percentages you choose to start with—they will soon right themselves as the game gets under way—but, for the sake of simplicity, choose multiples of 10 per cent for each ring, i.e., 10 per cent in ring i, 30 per cent in ring 2, 60 per cent in ring 3.

9. Now translate these percentages into actual densities of families per net acre. Since you will have to do this many times during the course of the game, it is advisable to construct a table which translates percentages directly into densities. You can make up such a table by inserting the values for N and R which you have chosen for your community into the formulae below. The formulae are based on the simple arithmetic of area, and population. R is expressed in hundreds of yards—roughly in blocks. The densities are expressed in families per gross acre. Multiply each ring density by a number between 1 and 10, according to the per cent in that ring. Thus, if there are 30 per cent in ring 3, the density there is 3 times the entry in the formulae, or 24N/57tR 2.