ВП СССР - Краткий курс...

Об этом часто забывают, описывая нечто как самодостаточную систему, явно или неявно опустив описание её отношений с объёмлющими системами, как процессами. Когда это приводит к очевидному ущербу вследствие деятельности на основе тех или иных описаний, то за такого рода ошибками следует другая ошибка: абсолютизация ошибочности прежнего описания.

Любое человеческое описание это — “калька” с Богом данной меры. Если мы входим в меру (через “ять”), то два любые числа приблизительно равны: вопрос только в том приемлема ли такая величина ошибки приближения, либо нет. То есть вопрос выявления неравенства это — вопрос Различения: в одних обстоятельствах пользоваться таким приблизительным равенством допустимо, а в других — нет. И это касается любого знания, зафиксированного как описания в культуре общества, будь то “второе начало термодинамики” или “балансовый метод” в задачах макроэкономики: Как пользоваться любыми описаниями и средствами описания — «языками» — так, чтобы ошибка, всегда порождаемая неадекватностью описаний первознанию и реальности, уходила бы в запас устойчивости безопасной деятельности?

Памятуя о существе этого вопроса, обратимся к линейной алгебре, как к средству описания производства и разпределения продукции на основе общественного объединения труда.

Разсмотрим рис. 1. На нём показано, как некий параметр X изменя­ется во времени t: — кривая I . Математически этот процесс идеально точно может моделироваться некой функцией X = f(t). Поскольку функция идеально точно моделирует реальный процесс, то её график— та же самая кривая I . Эта функция нелинейна, т.е. математически не может быть представлена как прямая линия или отрезок прямой (соответственно, график линейной функции представляет собой прямую или отрезок прямой). Ломаные I, II , III , IV‑I , IV‑II — различные линейные аппроксимации (т.е. описания) реальности и идеальной нелинейной функции X = f(t) линейной функцией (прямая III ) и кусочно-линейными (ломаные II , IV‑I , IV‑II ) функциями. Каждой из аппроксимаций свойственна некоторая ошибка.

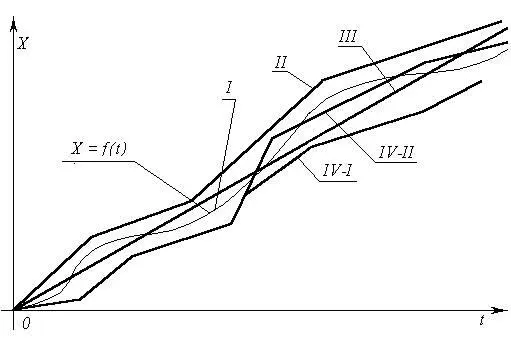
Можно предположить, что линейные аппроксимации изображают моделирование в процессе принятия управленческих решений; а кривая I изображает реальный процесс управления, в котором осуществлены управлен­ческие решения, выработанные на основе одного из линейных моделирований реально нелинейного управляемого процесса X = f(t) .

При любом значении аргумента t разность между кривой I и линейной аппроксимацией ( II , III , IV‑I , IV‑II ) — ошибка моделирования. Рис. 1 показывает не конкретное соотношение «модели­ро­вание — реализация», а типы возможного взаимного разположения моделирующих аппроксимаций и реализаций процесса управления. Могут быть задачи, в которых допустимо любое из показанных соотношений «моделирование — реализация».

Но могут быть задачи управления, в которых соотношения: « f(t) — аппроксимация III », « f(t) — аппроксимация IV‑II » недопустимы, посколь­ку ошибка моделирования в них изменяет свой знак в процессе реального управления. Таковы все задачи навигации: если ошибка моделирования меняет свой знак непредсказуемым образом, а знак ошибки неизвестен, то курс корабля реально может пролегать и через сушу, и через недопустимое мелководье; а самолёт врежется в посадочную полосу вместо того, чтобы мягко сесть на неё, если вообще не врежется в гору где-то по дороге из-за ошибки по высоте неопределённого знака.

Аппроксимации II , IV‑I сохраняют неизменным знак ошибки моделирования в процессе управления. В задачах управления макроэкономическими системами, аппроксимация II — это перенапряженный план, не обеспеченный мощностями и доступными ресурсами; а кривая I — реальное производство, которое не в силах перевалить через “рекордное задание”.

В задачах управления многоотраслевыми производственно-потреби­тель­скими системами, которое невозможно вести иначе как по схеме предиктор-корректор, приемлемое соотношение упреждающего модели­рования и реального процесса это — взаимное положение аппроксимации IV‑I и кривой I . Неизбежная ошибка моделирования присутствует, но она всегда имеет один и тот же знак, причем моделирующие аппроксимации лежат всегда ниже, чем кривая I , изображающая реальный процесс. Если это процесс производства, то никогда не будет произведено меньше, чем заказано или задано, что и требуется при подъёме производства до общественно необходимого уровня и изключает падение производства ниже допустимого при устойчивом достижении уровня общественно удовлетворительной достаточности.